16  S: Logistic Regression

Load R-libraries

Code 
# Load the library "rstanarm" to fit Bayesian linear models using the function  
# stan_glm() 

library(rstanarm)

Topics

  • Relative versus absolute risk
    • Risk
    • Odds
    • Risk difference
    • Relative risk (or risk ratio)
    • Odds ratio
  • Logistic regression.
    • Logistic regression model
    • Interpretation of coefficients

Readings:
Gelman et al. (2021), Chapter 13 covers logistic regression.


16.1 Relative and absolute risk

Before we go into the details of logistic regression, we need to clarify the meaning of common measures of binary outcomes and contrasts, specifically:

  • Risk (or prevalence, or proportion, or probability),
  • Odds,
  • Risk difference,
  • Relative risk (or risk ratio), and
  • Odds ratio.


Relationship probability (“risk”) and odds:

  • \(odds = \frac{p}{1 - p}\)
  • \(p = \frac{odds}{1 + odds}\)


Group Disease No disease row sum
1 a b a+b
0 c d c+d


  • Risk
    • \(Risk_{group 1} = a/(a+b)\)
    • \(Risk_{group 0} = c/(c+d)\)
  • Odds
    • \(Odds_{group 1} = Risk_{group 1} / (1 - Risk_{group 1}) = a/b\)
    • \(Odds_{group 0} = Risk_{group 0} / (1 - Risk_{group 0}) = c/d\)
  • Risk difference (RD)
    • \(RD = Risk_{group 1} - Risk_{group 0} = a/(a+b) - c/(c+d)\), or
    • \(RD = Risk_{group 0} - Risk_{group 1} = c/(c+d) - a/(a+b)\)
  • Relative risk (RR)
    • \(RR = Risk_{group 1} / Risk_{group 0} = \frac{a/(a+b)}{c/(c+d)}\), or
    • \(RR = Risk_{group 0} / Risk_{group 1} = \frac{c/(c+d)}{a/(a+b)}\)
  • Odds ratio (OR)
    • \(OR = Odds_{group 1} / Odds_{group 0} = \frac{a/b}{c/d} = \frac{ad}{bc}\), or
    • \(OR = Odds_{group 0} / Odds_{group 1} = \frac{c/d}{a/b} = \frac{bc}{ad}\)

Note: With low prevalence of disease (low risk), \(a\) is much smaller than \(b\), and \(c\) is much smaller than \(d\), and OR is similar to RR.

\(RR = \frac{a/(a+b)}{c/(c+d)} \approx \frac{a/b}{c/d} = OR\), if \(a \ll b, c \ll d\)

For large \(a\) and \(c\), \(OR > RR\)



Randomized controlled trial: Effect of aspirin on the incidence of heart attacks.

Group Heart attack No heart attack
Aspirin 104 10,933 11,037
Placebo 189 10,845 11,034
293 21,778 22,071


  • Risk
    • \(Risk_{aspirin} = 104/11037\) = 0.0094
    • \(Risk_{placebo} = 189/11034\) = 0.0171
  • Odds
    • \(Odds_{aspirin} = 104/10933\) = 0.0095
    • \(Odds_{placebo} = 189/10845\) = 0.0174
  • Risk difference (RD)
    • \(RD = Risk_{aspirin} - Risk_{placebo}\) = -0.0077
    • \(RD = Risk_{placebo} - Risk_{aspirin}\) = 0.0077
  • Relative risk (RR)
    • \(RR = Risk_{aspirin} / Risk_{placebo}\) = 0.5501
    • \(RR = Risk_{placebo} / Risk_{aspirin}\) = 1.8178
  • Odds ratio (OR)
    • \(OR = Odds_{aspirin} / Odds_{placebo}\) = 0.5458
    • \(OR = Odds_{placebo} / Odds_{aspirin}\) = 1.8321


16.2 Logistic regression

Logistic regression is used for binary outcome variables, typically coded 0 or 1, such as alive/dead, healthy/sick, successful/unsuccessful, correct/incorrect, etc.

Remember the general form of of the linear model:

\(y_i \sim Normal(\mu_i, \sigma)\)
\(\mu_i = b_0 + b_1x_i\)

Logistic regression can be defined similarly:

\(y_i \sim Bernoulli(p_i)\)
\(p_i = logit^{-1}(b_0 + b_1x_i)\)

Or equivalent (and more common):

\(y_i \sim Bernoulli(p_i)\)
\(logit(p_i) = b_0 + b_1x_i\)

Note that \(Bernoulli(p)\) is a special cases of the binomial distribution \(Binomial(n, p)\) with \(n = 1\).


The estimated parameter \(p_i\) is the probability (“risk”) of y = 1 given specific value(s) of the predictor(s) x. The probability \(p_i\) is also the mean, as the mean of an indicator variable y is the probability of y = 1. Thus, both the linear and the logistic model predicts the mean value of the outcome variable given a specific value of the predictor. A difference is that the estimated parameter \(\mu_i\) in the linear model is also a possible value of a single observation, whereas the estimated parameter \(p_i\) in logistic regression is a value that is never seen in a single observation, as these only can take on values of 0 or 1.


The logistic model involve a linear model. In theory, a line has no boundaries and can go from \(-\infty\) to \(\infty\), whereas a probability (or risk or proportion or prevalence) can only take values between 0 and 1. The way logistic regression deals with this is to make a linear model not of the probability, but of the unbounded log-odds:

  • \(p\)    \([0, 1]\)
  • \(odds = \frac{p}{1 - p}\)    \([0, \infty)\)
  • \(log(odds) = log(\frac{p}{1 - p})\)    \((-\infty, \infty)\)

The function that transforms \(p\) to log-odds is called

  • \(logit(p) = log(\frac{p}{1 - p})\)

The linear model is nested in the inverse logit, \(logit^{-1}\), that restricts the output of \(p\) to the interval [0, 1]:

  • \(p_i = logit^{-1}(b_0 + b_1x_i)\)

As seen in the left-hand figure below, when the output of the linear model (\(b_0 + b_1x_i\)) goes below -4 or above +4, the predicted probability (the output of the inverse-logit) is close to zero and one, respectively. When the linear model is zero, the probability is 0.5.


inverse-logit() and logit():

  • \(p = logit^{-1}(b_0 + b_1x_i) = \frac{e^{b_0 + b_1x_i}}{1 + e^{b_0 + b_1x_i}}\), or in R: plogis().
  • \(logit(p_i) = log(\frac{p_1}{1-pi}) = b_0 + b_ix_i\), or in R: qlogis()
Code 
par(mfrow = c(1, 2))

# Plot of logistic() = inv_logit()
x <- seq(-5, 5, by = 0.1)
p <- plogis(x)
plot(x, p, type = "l", xlab = "Linear model: b0 + b1x", 
     ylab = " p = inverse-logit(b0 + b1x)")
abline(0,0, col = "grey")
abline(1,0, col = "grey")
mtext(side = 3, text = "inverse-logit()", cex = 0.9)

# Plot of logit()
q <- qlogis(p)
plot(p, x, type = "l", xlab = "p", 
     ylab = "logit(p) = b0 + b1x")
mtext(side = 3, text = "logit()", cex = 0.9)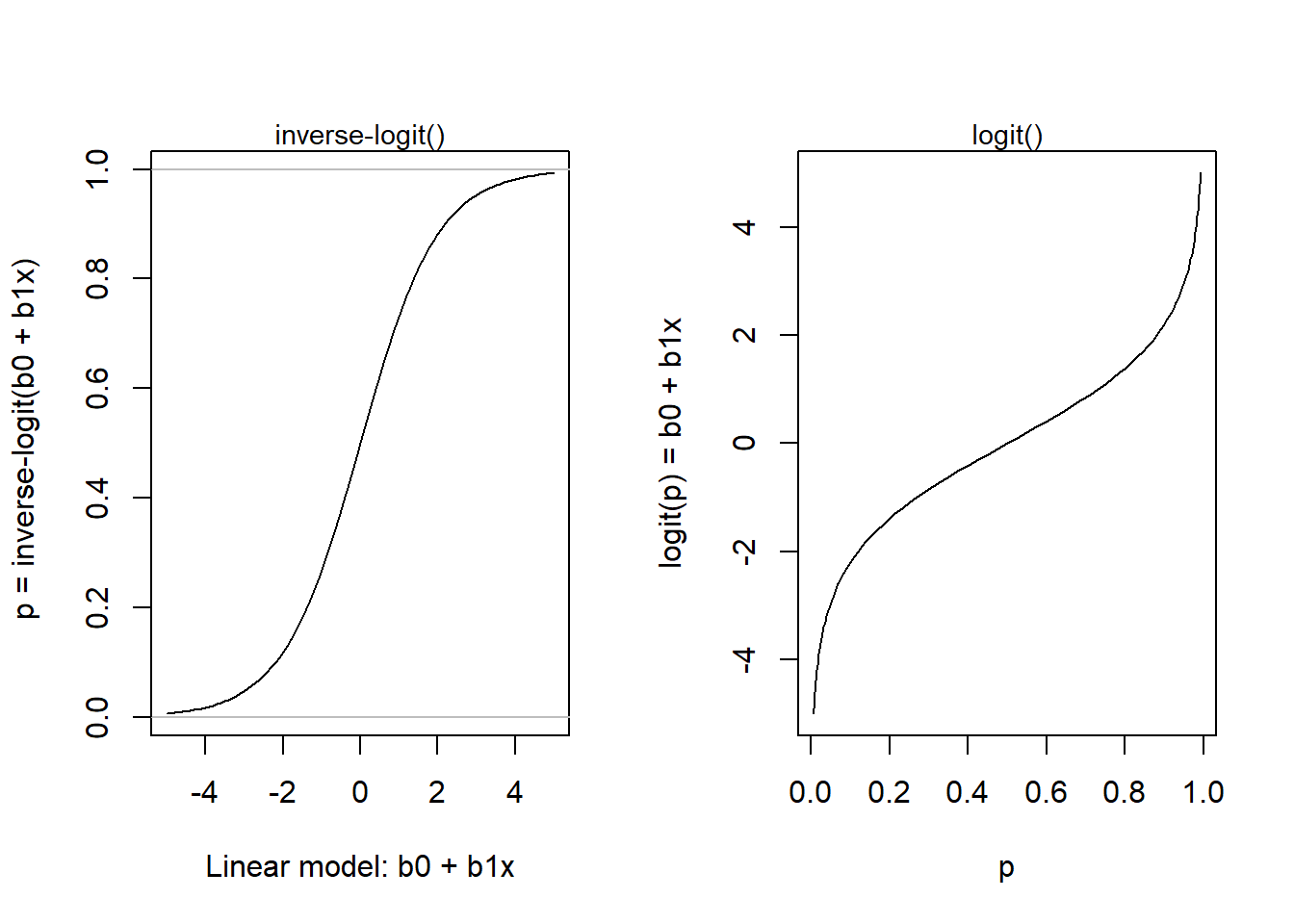


Here is an example from Gelman et al. (2021) (fig 13.1b. p, 218) for a simple model with one predictor:

\(y_i \sim Bernoulli(p_i)\)
\(p_i = logit^{-1}(-1.4 + 0.33x_i)\)

Code 
x <- seq(-20, 20, by = 0.1)
b0 <- -1.4
b1 <- 0.33
par(mfrow = c(1, 2))
plot(x, b0 + b1*x, type = 'l', ylab = "log-odds = -1.4 + 0.33x")
mtext(side = 3, text = "Linear model", cex = 0.9)
y <- (exp(b0 + b1*x) / (1 + exp(b0 + b1*x)))
plot(x, y, ylab = "p = inv-logit(-1.4 + 0.33x)", type = 'l', xlab = "x")
abline(0,0, col = "grey")
abline(1,0, col = "grey")
mtext(side = 3, text = "inv-logit(Linear model)", cex = 0.9)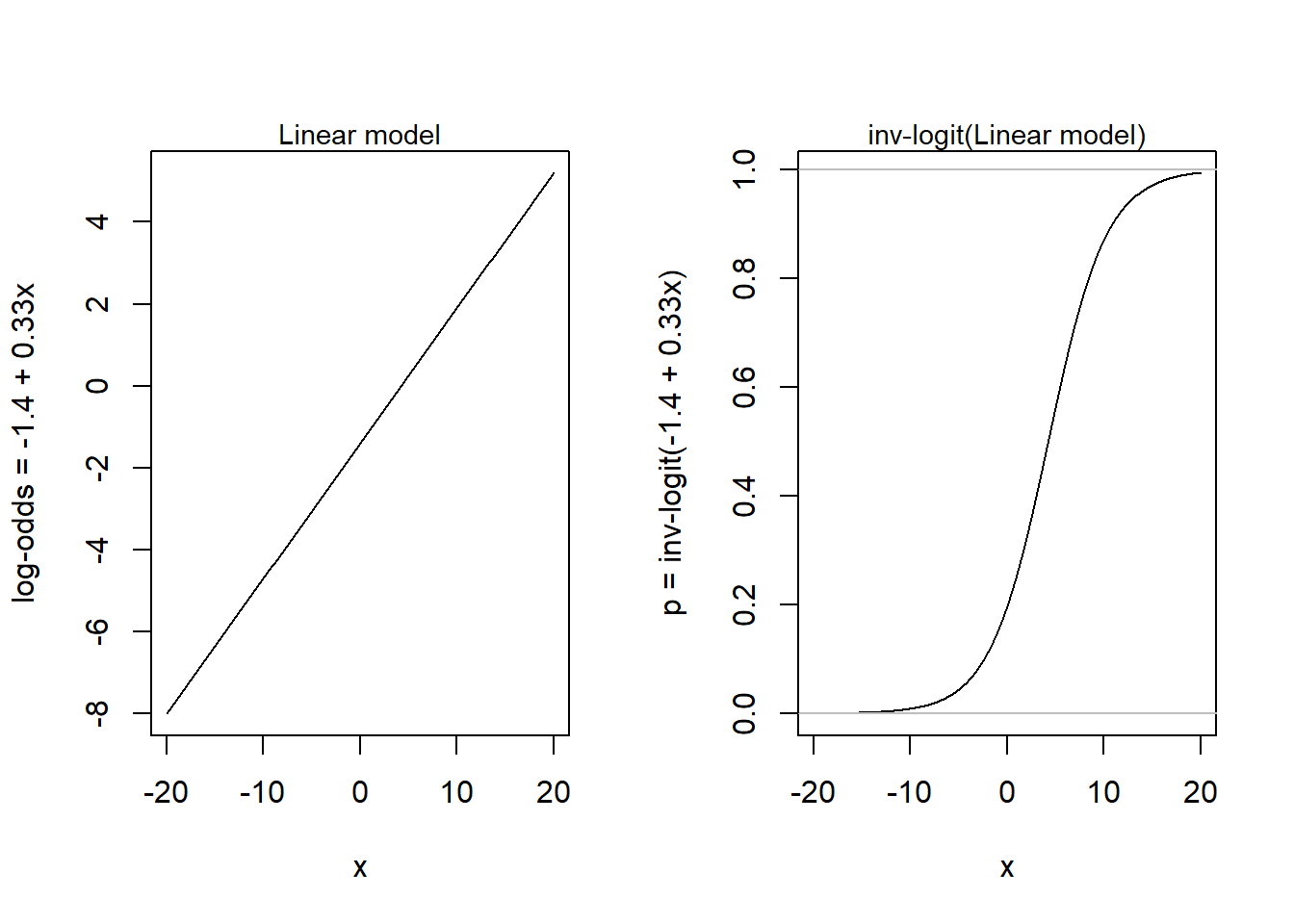


In their example, the function predicted the probability of supporting George Bush in the 1992 presidential election, as a function of income level from 1 to 5 (see their figure 13.2). But here I will assume another story, to justify looking at the function in its full range. So, let’s assume that y is a binary outcome variable indicating success (1) or failure (0) in solving a not too-easy mathematical problem, and x is a mean-centered variable representing the amount of mathematical training of the problem solver (-20 is the amount of training of a 7-year old school kid, +20 of a Ph.D. in mathematics, and 0 is the mean amount of training in the population).

Let’s simulate data, using rbinom(), plot data and fit data to a logistic model using glm() (please try rstanarm::stan_glm()). ``

Code 
# Simulate data
set.seed(123)
x <- rep(seq(-20, 20), 100)  # Exposure
pp <- plogis(-1.4 + 0.33*x)  # Probability of outcome = 1
y <- rbinom(length(x), 1, prob = pp) # Data: 0 or 1

# Plot, with transparent colors
jitter <- rnorm(length(x), 0, 0.02)
plot(x + jitter, y, xlim = c(-20, 20), ylim = c(0, 1), pch = 20, 
     col = rgb(0, 0, 1, 0.02), cex = 2, xlab = "x", ylab = "P(y = 1)")

# Model using glm()
m <- glm(y ~ x, family = binomial(link = "logit"))
xline <- seq(-20, 20, by = 0.1)
yline <- plogis(m$coefficients[1] + m$coefficients[2]*xline)
lines(xline, yline, col = "darkred", lwd = 2)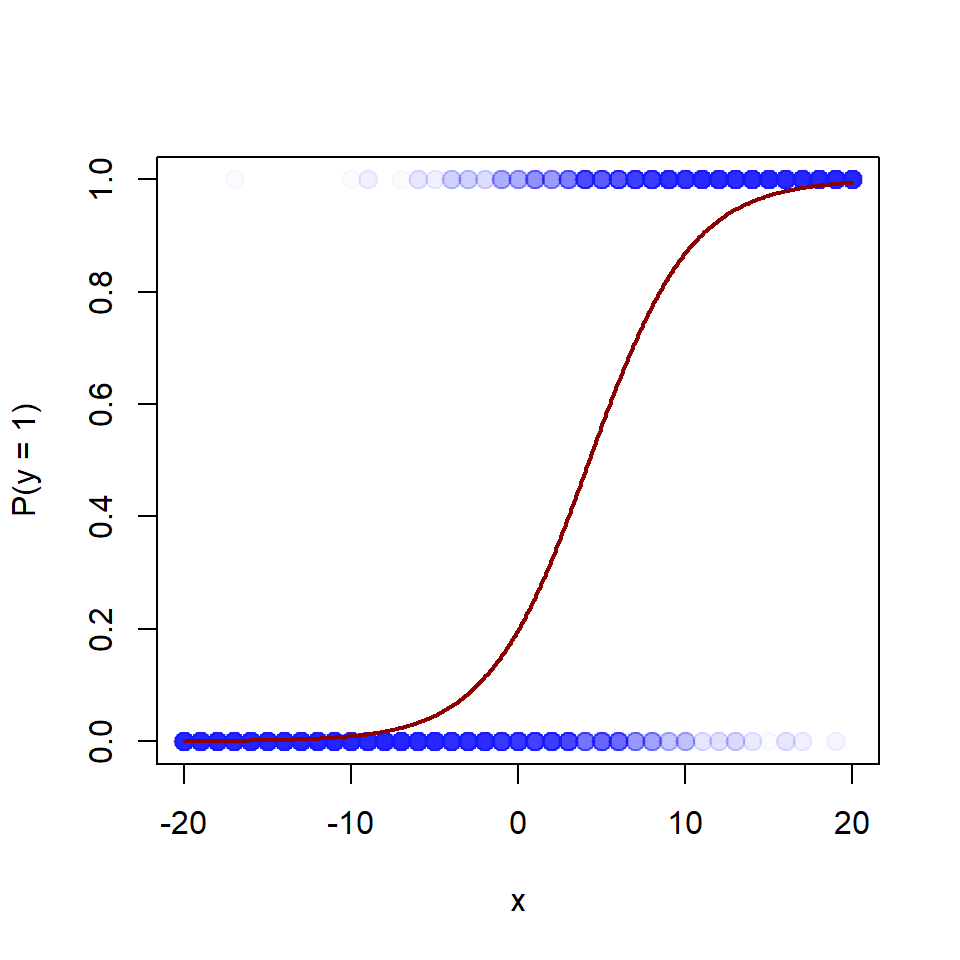

Code 
round(coef(m), 2)
(Intercept)           x 
      -1.40        0.33
Code 
round(confint(m), 2)
            2.5 % 97.5 %
(Intercept) -1.54  -1.26
x            0.31   0.35


Interpretations of intercept, \(b_0 = -1.4\)

  • This is the output (log-odds) of the linear model when x = 0, in this case for individuals with average mathematical training. Converting this to probability yields: \(\frac{exp(-1.4)}{1 + exp(-1.4)} \approx 0.2\). That is, according to the model, about 20 % of people with average amount of mathematical training would solve the mathematical problem.

Interpretations of slope, \(b_1 = 0.33\)

  • \(exp(b_1)\) is the odds ratio comparing groups defined by x and x+1. In the example above, \(b_1 = 0.33\), so \(exp(b_1) = 1.39 = \frac{Odds(y = 1|x+1)}{Odds(y = 1|x)}\) .
  • Interpretation of \(b_1\) in terms of relative risk (RR) or risk difference (RD) is more complicated. Unlike the odds ratio (OR), which is the same for any comparison of x with x+1, the RD and RR depend on the value of x for which the comparison is done, see illustration in figure below.
  • Rule-of-thumb for the risk difference: \(b_1/4\) is the upper limit for difference in risk, \(p\), between groups defined by x and x+1 (Gelman et al’s “Divide-by-4 rule”, p. 220). In the example above, \(b_1 = 0.33\) and \(b_1/4 = 0.08\), so a difference in one unit on x corresponds to a difference of at most 0.08 in \(p\) (i.e., risk difference of no more than 8 % for a one-unit difference in x).


Code 
b0 <- -1.4
b1 <- 0.33
x0 <- seq(-20, 20, by = 0.1)
y0 <- (exp(b0 + b1*x0) / (1 + exp(b0 + b1*x0)))
x1 <- x0 + 1
y1 <- (exp(b0 + b1*x1) / (1 + exp(b0 + b1*x1)))

rd <- y1 - y0
rr <- y1/y0
or <- (y1/(1-y1)) / (y0/(1-y0))

par(mfrow = c(1, 2))
# Data and logistic function
jitter <- rnorm(length(x), 0, 0.02)
plot(x + jitter, y, xlim = c(-20, 20), ylim = c(0, 1), pch = 20, 
     col = rgb(0, 0, 1, 0.02), cex = 1, xlab = "x", ylab = "Pr(y = 1|x)")
lines(x0, y0, col = "darkred")

# Effect measures: RD, RR, OR
plot(c(-20, 20), c(0, 2), pch = "", xlab = "x", 
     ylab = "Effect size per unit change in x")
lines(x0, rd, col = "blue", lty = 2)
lines(x0, rr, col = "red", lty = 3)
lines(x0, or, col = "darkgreen", lty = 4)

# Add text to fig
text(x = -20, y = 0.1, labels = "Risk difference", 
     pos = 4, cex = 0.7, col = "blue")
text(x = 8, y = 0.95, labels = "Relative risk", 
     pos = 4, cex = 0.7, col = "red")
text(x = 8, y = 1.45, labels = "Odds ratio", 
     pos = 4, cex = 0.7, col = "darkgreen")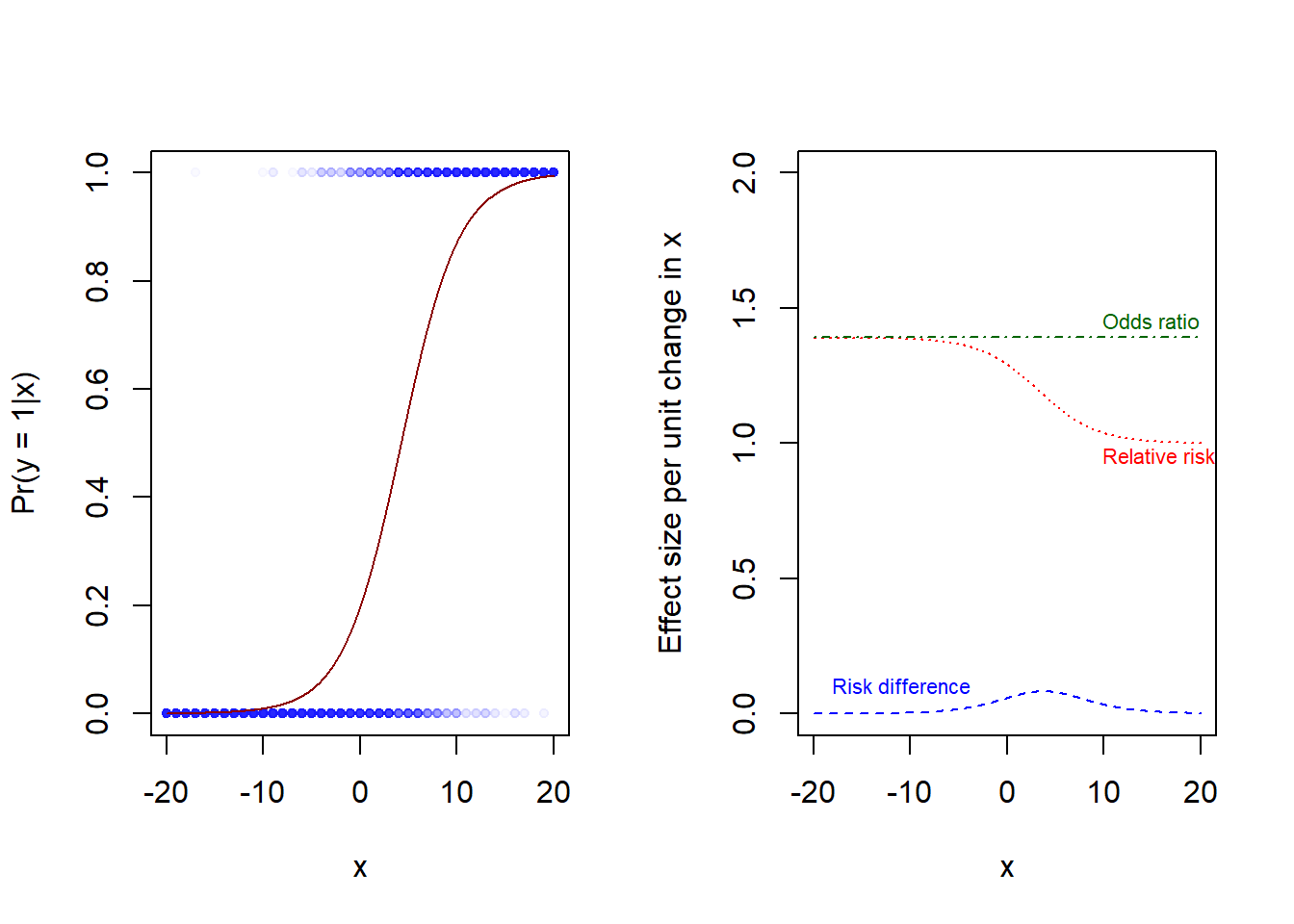


Logistic regression with just an intercept

As we noted earlier for linear regression (Notes 10): Estimating the mean is the same as regressing on a constant.

\(y_i \sim Normal(\mu, \sigma)\)
\(\mu = b_0\),

where \(b_0\) is the estimate of the population mean.

The same holds for logistic regression, where the mean is the probability of y = 1.

\(y_i \sim Bernoulli(p)\)
\(p = logit^{-1}(b_0)\),

where \(b_0\) is the log-odds, and \(p = logit^{-1}(b_0) = \frac{exp(b_0)}{1 + exp(b_0)}\)

In the Aspirin experiment, the overall (marginal) proportion of heart attacks was 293 in 22,070 (so the sample proportion equals 0.013). We could use logistic regression to estimate the population proportion with a compatibility interval.

Code 
# Data from aspirin experiment
mi <- c(rep(1, 104), rep(0, 10933), rep(1, 189), rep(0, 10845))
aspirin <- c(rep(1, 104), rep(1, 10933), rep(0, 189), rep(0, 10845))
a <- data.frame(aspirin, mi)

# Fit intercpt-only model, display coefficients (log-odds)  
asp0 <- glm(mi ~ 1, family = binomial(link ="logit"), data = a)
coef(asp0)
(Intercept) 
  -4.308483
Code 
confint(asp0)
Waiting for profiling to be done...
    2.5 %    97.5 % 
-4.425954 -4.195331
Code 
# Display as probabilities, using the inverse-logit, in R called plogis()
plogis(coef(asp0))
(Intercept) 
 0.01327534
Code 
plogis(confint(asp0))
Waiting for profiling to be done...
     2.5 %     97.5 % 
0.01182137 0.01484215


Logistic regression with a single binary predictor

And as we noted earlier for linear regression (Notes 10): Estimating a difference between two means is the same as regressing on an indicator variable:

\(y_i ~ Normal(\mu_i, \sigma)\)
\(\mu_i = b_0 + b_iD_i\),

where \(D_i\) is an indicator variable coded 0 for one group and 1 for the other. Thus, \(b_0\) is the estimate of the population mean for group 0, and \(b_1\) is an estimate of the difference between population group means.

Similarly for logistic regression:

\(y_i ~ Bernouilli(p_i)\)
\(p_i = logit^{-1}(b_0 + b_iD_i)\).

Here \(b_0\) is the log-odds of group 0, and \(b_i\) is the difference in log-odds between the two groups. Note that \(exp(b_1)\) is the odds ratio of group 1 versus group 0. We may also convert to probabilities:

  • Probability y = 1 for group 0: \(Pr(y = 1|D = 0) = logit^{-1}(b_0) = \frac{exp(b_0)}{1 + exp(b_0)}\)
  • Probability y = 1 for group 1: \(Pr(y = 1|D = 1) = logit^{-1}(b_0 + b_1) = \frac{exp(b_0 + b_1)}{1 + exp(b_0 + b_1)}\)

Here I create a data frame with as many rows as participants in the Aspirin experiment (see Table above), and then I use logistic regression to fit the model (MI for myocardial infarction, coded 0 or 1)

\(MI_i \sim Bernouilli(p_i)\)
\(p_i = logit^{-1}(b_0 + b_1Aspirin_i)\)

Code 
# Data from aspirin experiment
mi <- c(rep(1, 104), rep(0, 10933), rep(1, 189), rep(0, 10845))
aspirin <- c(rep(1, 104), rep(1, 10933), rep(0, 189), rep(0, 10845))
a <- data.frame(aspirin, mi)
table(aspirin = a$aspirin, mi = a$mi)
       mi
aspirin     0     1
      0 10845   189
      1 10933   104
Code 
# Logistic regression
aspfit <- glm(mi ~ aspirin, family = binomial(link ="logit"), data = a)
summary(aspfit)

Call:
glm(formula = mi ~ aspirin, family = binomial(link = "logit"), 
    data = a)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -4.04971    0.07337 -55.195  < 2e-16 ***
aspirin     -0.60544    0.12284  -4.929 8.28e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 3114.7  on 22070  degrees of freedom
Residual deviance: 3089.3  on 22069  degrees of freedom
AIC: 3093.3

Number of Fisher Scoring iterations: 7


Converting \(b_0\) to risk for placebo group, \(b_1\) to odds ratio: aspirin/placebo, and \(b_0 + b_1\) to risk of aspirin group.

Code 
# Coefficients
b0 <- aspfit$coefficients[1]
b1 <- aspfit$coefficients[2]

# Transform using plogis() and exp()
asp_estimates <-        c(plogis(b0),      plogis(b0+b1),    exp(b1))
names(asp_estimates) <- c("risk-placebo", "risk-aspirin", "odds ratio")
round(asp_estimates, 4)
risk-placebo risk-aspirin   odds ratio 
      0.0171       0.0094       0.5458


16.3 Arsenic data

Here example from Gelman et al. (2021) from arsenic level in wells in Bangladesh and users decisions to switch to less polluted wells, for details, see p. 234-237.

Follow this link to find data Save (Ctrl+S on a PC) to download as text file


Code book:

Measurements of wells and households, and follow registration of well-switching behavior at follow up a few years later.

  • switch Whether the household had switched wells at follow up.
  • arsenic Arsenic level in units of hundreds of microgram per liter. Levels below 0.5 are considered “safe”.
  • dist Distance in meters to closets safe well.
  • dist100 dist/100, so unit is 100-m.
  • assoc Whether any members of the household are active in community organizations.
  • educ The education level ff the household (years of education).
  • educ4 educ/4, so units i 4y-education.


Import data

Code 
# Import data
wells <- read.table("datasets/wells.txt", header = TRUE, sep = ",")
str(wells)
'data.frame':   3020 obs. of  7 variables:
 $ switch : int  1 1 0 1 1 1 1 1 1 1 ...
 $ arsenic: num  2.36 0.71 2.07 1.15 1.1 3.9 2.97 3.24 3.28 2.52 ...
 $ dist   : num  16.8 47.3 21 21.5 40.9 ...
 $ dist100: num  0.168 0.473 0.21 0.215 0.409 ...
 $ assoc  : int  0 0 0 0 1 1 1 0 1 1 ...
 $ educ   : int  0 0 10 12 14 9 4 10 0 0 ...
 $ educ4  : num  0 0 2.5 3 3.5 2.25 1 2.5 0 0 ...


Summary

Code 
summary(wells, digits = 2)
     switch        arsenic          dist           dist100           assoc     
 Min.   :0.00   Min.   :0.51   Min.   :  0.39   Min.   :0.0039   Min.   :0.00  
 1st Qu.:0.00   1st Qu.:0.82   1st Qu.: 21.12   1st Qu.:0.2112   1st Qu.:0.00  
 Median :1.00   Median :1.30   Median : 36.76   Median :0.3676   Median :0.00  
 Mean   :0.58   Mean   :1.66   Mean   : 48.33   Mean   :0.4833   Mean   :0.42  
 3rd Qu.:1.00   3rd Qu.:2.20   3rd Qu.: 64.04   3rd Qu.:0.6404   3rd Qu.:1.00  
 Max.   :1.00   Max.   :9.65   Max.   :339.53   Max.   :3.3953   Max.   :1.00  
      educ          educ4    
 Min.   : 0.0   Min.   :0.0  
 1st Qu.: 0.0   1st Qu.:0.0  
 Median : 5.0   Median :1.2  
 Mean   : 4.8   Mean   :1.2  
 3rd Qu.: 8.0   3rd Qu.:2.0  
 Max.   :17.0   Max.   :4.2


Model with only distance as predictor

Code 
fit_1 <- stan_glm(switch ~ dist100, family = binomial(link = "logit"), 
                  data = wells, refresh = 0)
print(fit_1, digits = 1)
stan_glm
 family:       binomial [logit]
 formula:      switch ~ dist100
 observations: 3020
 predictors:   2
------
            Median MAD_SD
(Intercept)  0.6    0.1  
dist100     -0.6    0.1  

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg


Visualize data and model prediction.

Code 
# function to jitter data points
jitter_binary <- function(a, jitt = 0.05){
  ifelse(a == 0, runif(length(a), 0, jitt), runif(length(a), 1- jitt, 1))
}

wells$switch_jitter <- jitter_binary(wells$switch)

# Plot jittered data
plot(wells$dist100, wells$switch_jitter, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Distance (in 100-m) to nearest safe well",
     ylab = "Pr(switching | distance)")
cf <- coef(fit_1)
x <- seq(from = 0, to = 4, by = 0.1)
ypred <- plogis(cf[1] + cf[2]*x)
lines(x, ypred)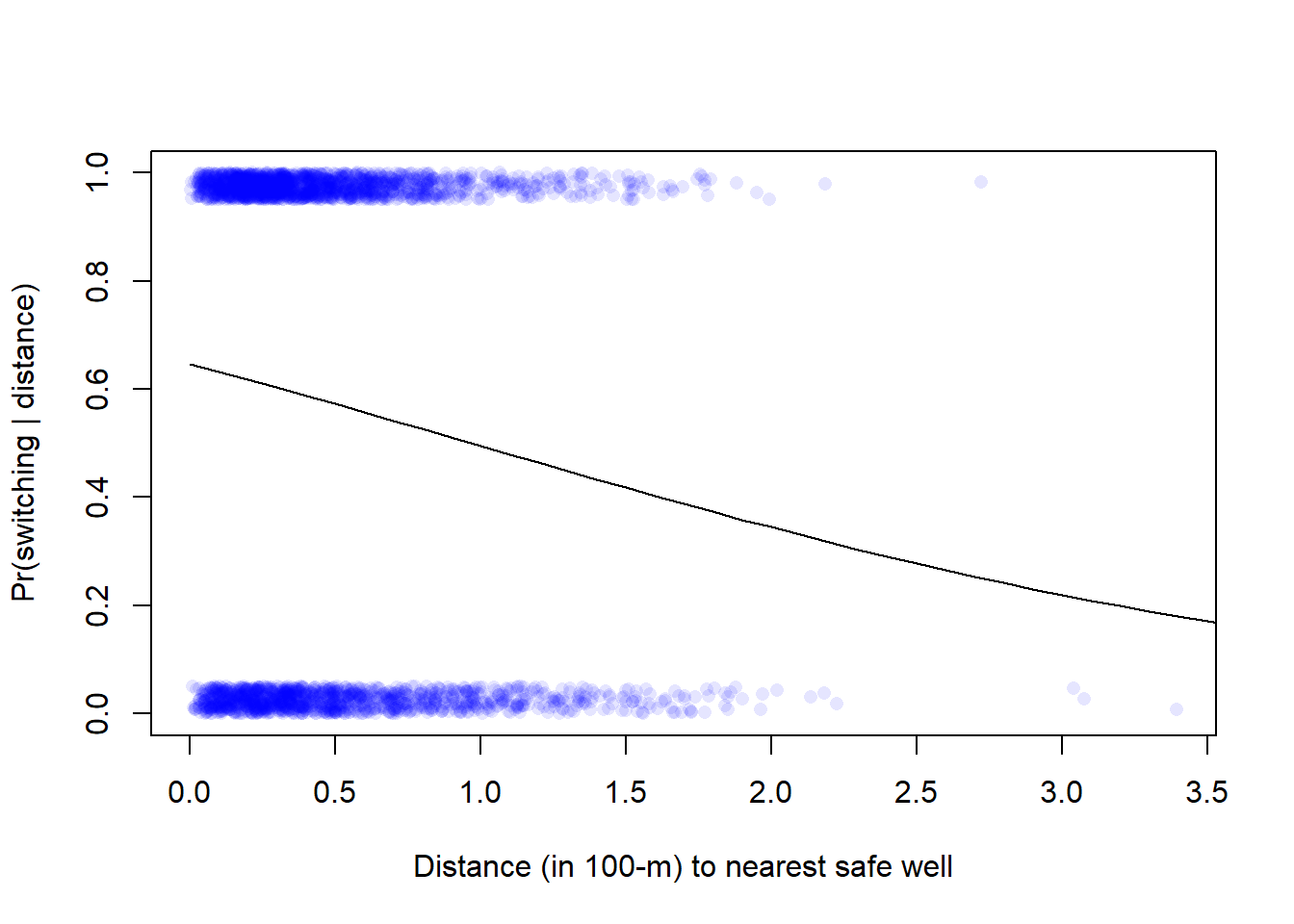


Model with distance and arsenic level as predictor

This is Gelman Fig. 13.10a

Code 
# Fit model (Gelman et al. calls it fit_3)
fit_3 <- stan_glm(switch ~ dist100 + arsenic, family = binomial(link = "logit"), 
                  data = wells, refresh = 0)
print(fit_3, digits = 2)
stan_glm
 family:       binomial [logit]
 formula:      switch ~ dist100 + arsenic
 observations: 3020
 predictors:   3
------
            Median MAD_SD
(Intercept)  0.00   0.08 
dist100     -0.90   0.10 
arsenic      0.46   0.04 

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg
Code 
# Plot data, see Fig. 13.10 (left) in Gelman et al.
plot(wells$dist100, wells$switch_jitter, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Distance (in 100-m) to nearest safe well",
     ylab = "Pr(switching | distance)")

# Model predictions, in data-frame called xx
cf <- coef(fit_3)
x <- seq(from = 0, to = 4, by = 0.1)
arsenic <- c(0.5, 1)
xx <- expand.grid(dist100 = x, arsenic = arsenic)
xx$ypred <- plogis(cf[1] + cf[2]*xx$dist100 + cf[3]*xx$arsenic)
head(xx)
  dist100 arsenic     ypred
1     0.0     0.5 0.5582066
2     0.1     0.5 0.5359890
3     0.2     0.5 0.5136276
4     0.3     0.5 0.4912115
5     0.4     0.5 0.4688307
6     0.5     0.5 0.4465747
Code 
# Add lines for model prediction with two levels of arsenic (low = 0.5, high = 1)
lines(xx$dist100[xx$arsenic == 0.5], xx$ypred[xx$arsenic == 0.5], lty = 2)
lines(xx$dist100[xx$arsenic == 1], xx$ypred[xx$arsenic == 1], lty = 1)

# Add text to plot
text(x = 0.5, y = 0.53, labels = "If As = 1", pos = 4, cex = 0.8)
text(x = 0.3, y = 0.37, labels = "If As = 0.5", pos = 4, cex = 0.8)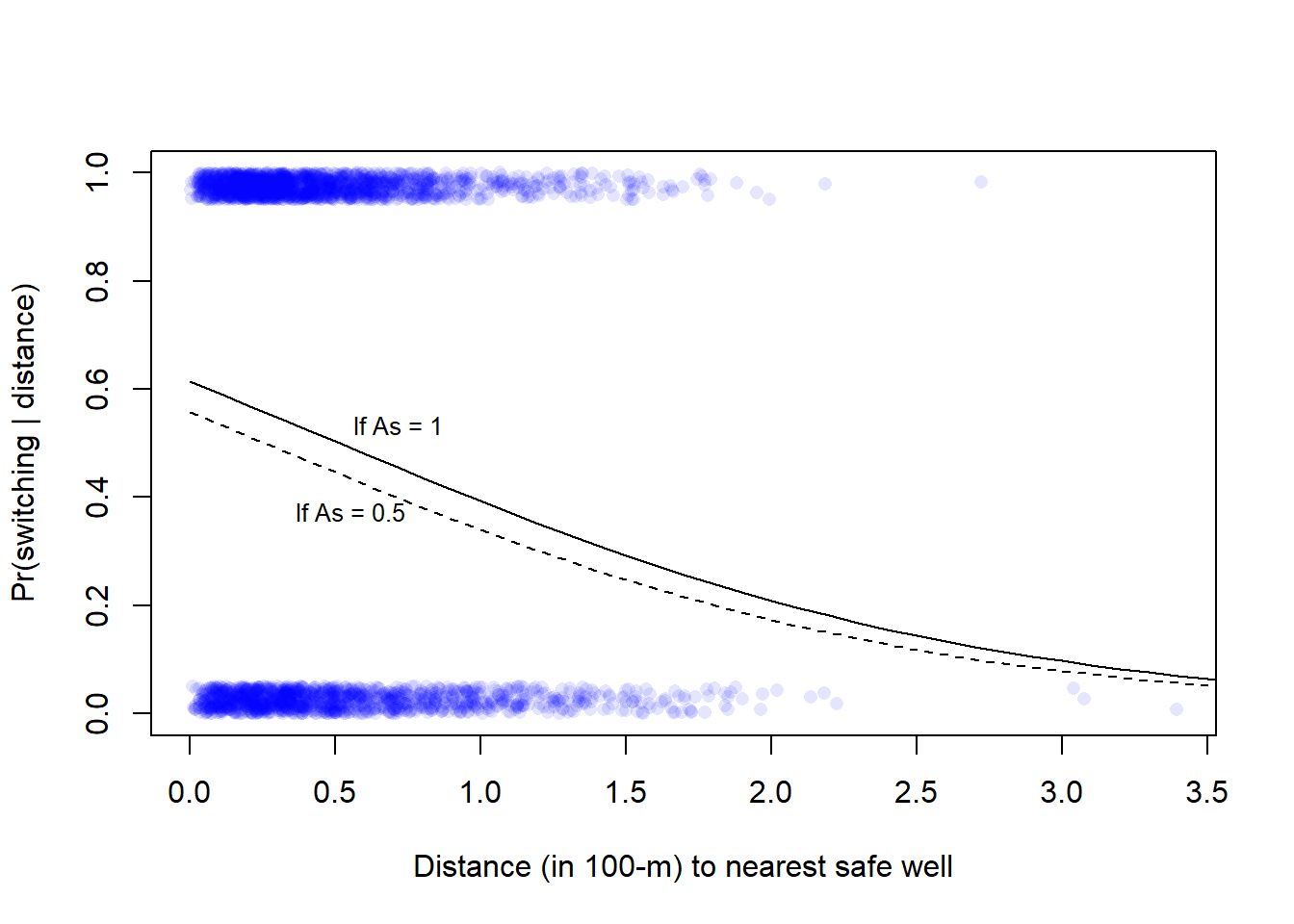


Here with lines for arsenic-level corresponding to the 5, 50, and 95th percentile, respectively. I show it on the log-odds scale (left) and on the the probability scale (as Gelman et al).

Code 
par(mfrow = c(1, 2))

## Plot, with outcome on log-odds scale ----
plot(NULL, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Distance (in 100-m) to nearest safe well",
     ylab = "log-odds (Pr(switching | distance))", 
     xlim = c(0, 4), ylim = c(-6, 6))

# Model predictions, in data-frame called xx
cf <- coef(fit_3)
x <- seq(from = 0, to = 4, by = 0.1)
arsenic <- quantile(wells$arsenic, c(0.05, 0.5, 0.95))
xx <- expand.grid(dist100 = x, arsenic = arsenic)
xx$ypred <-cf[1] + cf[2]*xx$dist100 + cf[3]*xx$arsenic
head(xx)
  dist100 arsenic        ypred
1     0.0    0.56  0.261520296
2     0.1    0.56  0.171838913
3     0.2    0.56  0.082157530
4     0.3    0.56 -0.007523853
5     0.4    0.56 -0.097205236
6     0.5    0.56 -0.186886619
Code 
# Add lines for model prediction with three levels of arsenic (5, 50, 95th)
lines(xx$dist100[xx$arsenic == arsenic[1]], xx$ypred[xx$arsenic == arsenic[1]], lty = 1)
lines(xx$dist100[xx$arsenic == arsenic[2]], xx$ypred[xx$arsenic == arsenic[2]], lty = 2)
lines(xx$dist100[xx$arsenic == arsenic[3]], xx$ypred[xx$arsenic == arsenic[3]], lty = 3)

# Add text to plot
text(x = 0.5, y = -1.7, labels = paste("As:", round(arsenic[1], 2)), pos = 4, cex = 0.8)
text(x = 0.5, y = 0.35, labels = paste("As:", round(arsenic[2], 2)), pos = 4, cex = 0.8)
text(x = 0.3, y = 1.8, labels = paste("As:", round(arsenic[3], 2)), pos = 4, cex = 0.8)


## Plot data, probability scale see Fig. 13.10 (left) in Gelman et al. ----
plot(wells$dist100, wells$switch_jitter, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Distance (in 100-m) to nearest safe well",
     ylab = "Pr(switching | distance)")

# Model predictions, in data-frame called xx
cf <- coef(fit_3)
x <- seq(from = 0, to = 4, by = 0.1)
arsenic <- quantile(wells$arsenic, c(0.05, 0.5, 0.95))
xx <- expand.grid(dist100 = x, arsenic = arsenic)
xx$ypred <- plogis(cf[1] + cf[2]*xx$dist100 + cf[3]*xx$arsenic)
head(xx)
  dist100 arsenic     ypred
1     0.0    0.56 0.5650100
2     0.1    0.56 0.5428543
3     0.2    0.56 0.5205278
4     0.3    0.56 0.4981190
5     0.4    0.56 0.4757178
6     0.5    0.56 0.4534139
Code 
# Add lines for model prediction with three levels of arsenic (5, 50, 95th)
lines(xx$dist100[xx$arsenic == arsenic[1]], xx$ypred[xx$arsenic == arsenic[1]], lty = 1)
lines(xx$dist100[xx$arsenic == arsenic[2]], xx$ypred[xx$arsenic == arsenic[2]], lty = 2)
lines(xx$dist100[xx$arsenic == arsenic[3]], xx$ypred[xx$arsenic == arsenic[3]], lty = 3)

# Add text to plot
text(x = 0.5, y = 0.25, labels = paste("As:", round(arsenic[1], 2)), pos = 4, cex = 0.8)
text(x = 0.5, y = 0.55, labels = paste("As:", round(arsenic[2], 2)), pos = 4, cex = 0.8)
text(x = 0.3, y = 0.85, labels = paste("As:", round(arsenic[3], 2)), pos = 4, cex = 0.8)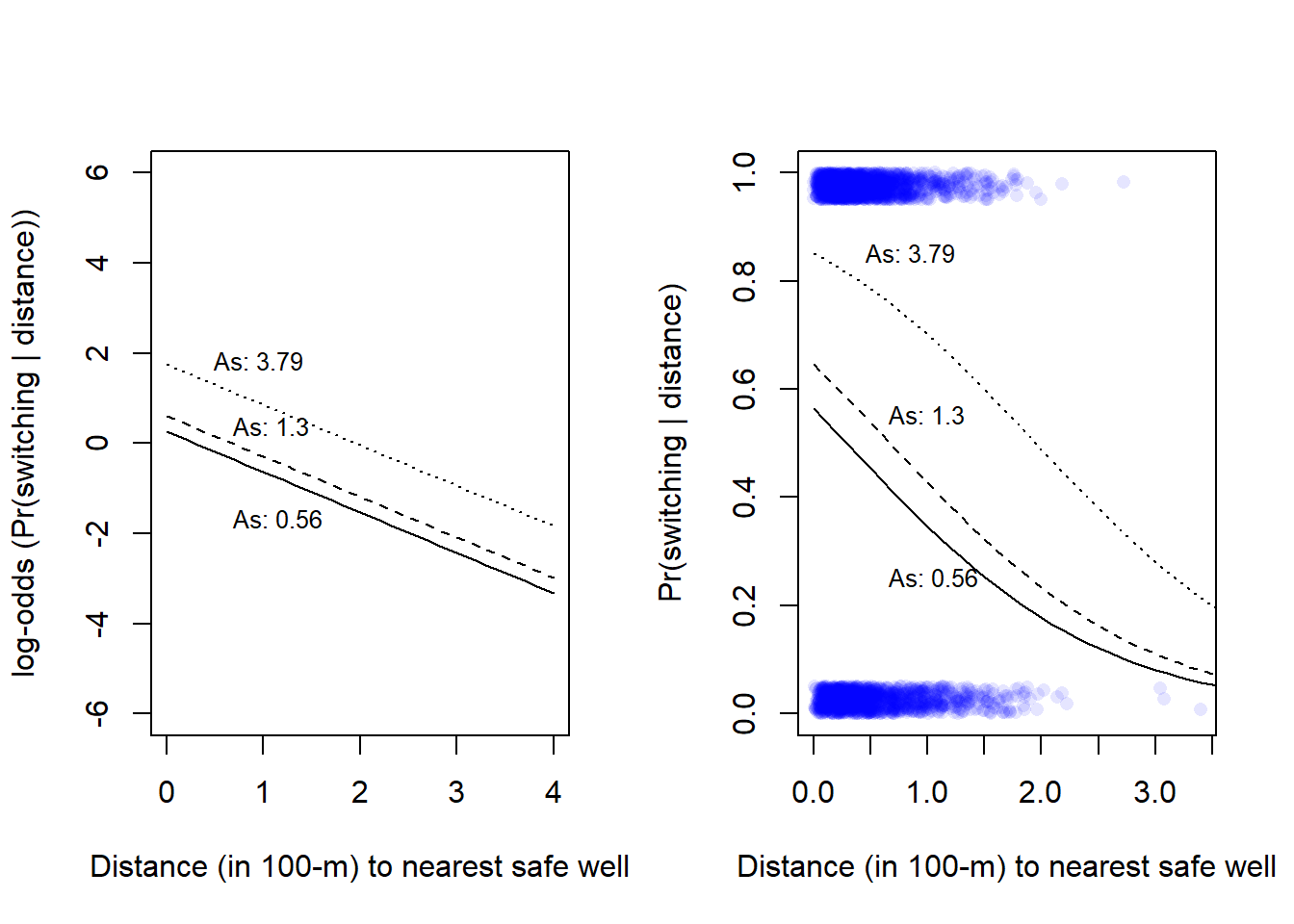

Code 
# print arsenic levels displayed
round(c(As = arsenic), 2)
 As.5% As.50% As.95% 
  0.56   1.30   3.79


Here with lines for distances corresponding to the 5, 50, and 95th percentile, respectively (cf. Gelman et al., Fig 13.10b).

Code 
# Probability scale, see Fig. 13.10 (left) in Gelman et al.
# Plot data, 
plot(wells$arsenic, wells$switch_jitter, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Arsenic concentration in well water",
     ylab = "Pr(switching | distance)", xlim = c(0, 8))

# Model predictions, in data-frame called xx
cf <- coef(fit_3)
x <- seq(from = 0.5, to = 8, by = 0.1)  # arsenic levels from 0 to 6
dist100 <- quantile(wells$dist100, c(0.05, 0.5, 0.95))
xx <- expand.grid(arsenic = x, dist100 = dist100)
xx$ypred <- plogis(cf[1] + cf[2]*xx$dist100 + cf[3]*xx$arsenic)
head(xx)
  arsenic   dist100     ypred
1     0.5 0.0798645 0.5404770
2     0.6 0.0798645 0.5518923
3     0.7 0.0798645 0.5632531
4     0.8 0.0798645 0.5745479
5     0.9 0.0798645 0.5857655
6     1.0 0.0798645 0.5968948
Code 
# Add lines for model prediction with three levels of dist100 (5, 50, 95th)
lines(xx$arsenic[xx$dist100 == dist100[1]], xx$ypred[xx$dist100 == dist100[1]], lty = 1)
lines(xx$arsenic[xx$dist100 == dist100[2]], xx$ypred[xx$dist100 == dist100[2]], lty = 2)
lines(xx$arsenic[xx$dist100 == dist100[3]], xx$ypred[xx$dist100 == dist100[3]], lty = 3)

# Add text to plot
text(x = 0.5, y = 0.28, labels = paste("Dist:", round(100*arsenic[1]), "m"), 
     pos = 4, cex = 0.8)
text(x = 0.5, y = 0.47, labels = paste("Dist:", round(100*arsenic[2]), "m"), 
     pos = 4, cex = 0.8)
text(x = 0.3, y = 0.65, labels = paste("Dist:", round(100*arsenic[3]), "m"), 
     pos = 4, cex = 0.79)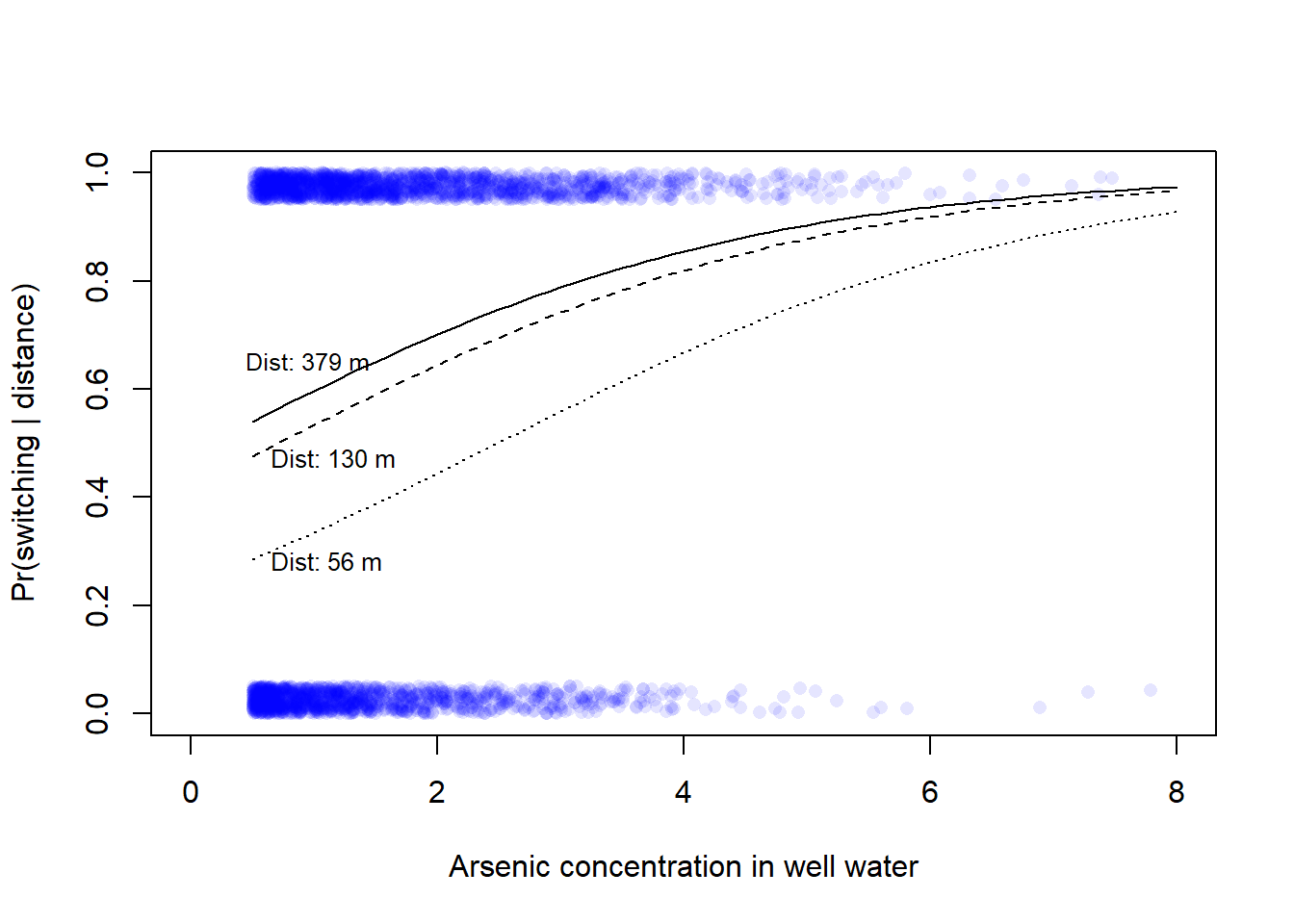


Add interaction term to the model. Below with no centering.

Code 
# Fit model (Gelman et al. calls it fit_4)
fit_4 <- stan_glm(switch ~ dist100 + arsenic + dist100:arsenic, 
                 family = binomial(link = "logit"), 
                  data = wells, refresh = 0)
print(fit_4, digits = 2)
stan_glm
 family:       binomial [logit]
 formula:      switch ~ dist100 + arsenic + dist100:arsenic
 observations: 3020
 predictors:   4
------
                Median MAD_SD
(Intercept)     -0.15   0.12 
dist100         -0.57   0.22 
arsenic          0.56   0.07 
dist100:arsenic -0.18   0.11 

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg


To help interpretation of coefficients, here the same model with centered predictors

Code 
# Centering
wells$c_dist100 <- wells$dist100 - mean(wells$dist100)
wells$c_arsenic <- wells$arsenic - mean(wells$arsenic)

# Model (Gelman et al. calls it fit_5, p. 244)
fit_5 <- stan_glm(switch ~ c_dist100 + c_arsenic + c_dist100:c_arsenic, 
                 family = binomial(link = "logit"), 
                  data = wells, refresh = 0)
print(fit_5, digits = 2)
stan_glm
 family:       binomial [logit]
 formula:      switch ~ c_dist100 + c_arsenic + c_dist100:c_arsenic
 observations: 3020
 predictors:   4
------
                    Median MAD_SD
(Intercept)          0.35   0.04 
c_dist100           -0.88   0.11 
c_arsenic            0.47   0.04 
c_dist100:c_arsenic -0.18   0.10 

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg
Code 
pred5 <- fitted(fit_5)  # Fitted value
res5 <- wells$switch - pred5  # Residual


Interpretation of the coefficients:

  • Intercept   The estimated log-odds of switching if distance and arsenic is at their means (c_dist100 = 0 and c_arsenic = 0). Use \(logit^{-1}(Intercept)\) to express in probability units, in R you may use plogis(). In the model above, the intercept is 0.35, so the models estimate of the probability of switching if distance and arsenic is at their mean is plogis(0.35) or about 0.59.
  • c_dist100   Coefficient for distance on the logit scale (i.e., log-odds) if arsenic level is at its mean. We can use the divide-by-4 rule to see that one unit increase in dist100 would correspond to at most a difference of -0.22 on the probability scale (if interpreted causally, a reduction in probability of switching)
  • c_arsenic   Coefficient for arsenic on the logit scale (i.e., log-odds) if dist100 at its mean. We can use the divide-by-4 rule to see that one unit increase in c_arsenic would correspond to at most a difference of +0.12 on the probability scale (if interpreted causally, a reduction in probability of switching)
  • c_dist100:c_arsenic.   Can be seen in two ways:
    • For each additional unit of arsenic, the value -0.18 is added to the coefficient for distance. The coefficient is negative (-0.88), larger distance means lower probability of switching. This negative relationship will be stronger for each additional unit of arsenic.
    • For each additional unit of distance, the value -0.18 is added to the coefficient for arsenic. The coefficient is positive (0.47), higher levels means higher probability of switching. This positive relationship will be weaker for each additional unit of distance.


Plot the model (only way to really understand the interaction), left on the log-odds scale, right on the probability scale.

Code 
par(mfrow = c(1, 2))

## Plot, with outcome on log-odds scale ----
plot(NULL, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Mean-centered dist100",
     ylab = "log-odds (Pr(switching | distance))", 
     xlim = c(-1, 3.5), ylim = c(-6, 6))

# Model predictions, in data-frame called xx
cf <- coef(fit_5)
x <- seq(from = -0.5, to = 3, by = 0.1)
arsenic <- quantile(wells$c_arsenic, c(0.05, 0.5, 0.95))
xx <- expand.grid(c_dist100 = x, c_arsenic = arsenic)
xx$dxa <- xx$c_dist100*xx$c_arsenic
xx$ypred <- cf[1] + cf[2]*xx$c_dist100 + cf[3]*xx$c_arsenic + cf[4]*xx$dxa
head(xx)
  c_dist100 c_arsenic       dxa       ypred
1      -0.5  -1.09693 0.5484652  0.17707787
2      -0.4  -1.09693 0.4387722  0.10901440
3      -0.3  -1.09693 0.3290791  0.04095093
4      -0.2  -1.09693 0.2193861 -0.02711253
5      -0.1  -1.09693 0.1096930 -0.09517600
6       0.0  -1.09693 0.0000000 -0.16323946
Code 
# Add lines for model prediction with three levels of arsenic (5, 50, 95th)
lines(xx$c_dist100[xx$c_arsenic == arsenic[1]], xx$ypred[xx$c_arsenic == arsenic[1]], lty = 1)
lines(xx$c_dist100[xx$c_arsenic == arsenic[2]], xx$ypred[xx$c_arsenic == arsenic[2]], lty = 2)
lines(xx$c_dist100[xx$c_arsenic == arsenic[3]], xx$ypred[xx$c_arsenic == arsenic[3]], lty = 3)

# Add text to plot
#text(x = -1, y = 0, labels = paste("As:", round(arsenic[1], 2)), pos = 4, cex = 0.8)
#text(x = -1, y = 0.7, labels = paste("As:", round(arsenic[2], 2)), pos = 4, cex = 0.8)
#text(x = -1, y = 2.2, labels = paste("As:", round(arsenic[3], 2)), pos = 4, cex = 0.8)


## Plot data, probability scale see Fig. 13.10 (left) in Gelman et al. ----
plot(NULL, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Mean-centered dist100",
     ylab = "Pr(switching | distance)", 
     xlim = c(-1, 3.5), ylim = c(0, 1))

# Model predictions, in data-frame called xx
cf <- coef(fit_5)
x <- seq(from = -0.5, to = 3, by = 0.1)
arsenic <- quantile(wells$c_arsenic, c(0.05, 0.5, 0.95))
xx <- expand.grid(c_dist100 = x, c_arsenic = arsenic)
xx$dxa <- xx$c_dist100*xx$c_arsenic
xx$ypred <- plogis(cf[1] + cf[2]*xx$c_dist100 + cf[3]*xx$c_arsenic + cf[4]*xx$dxa)
head(xx)
  c_dist100 c_arsenic       dxa     ypred
1      -0.5  -1.09693 0.5484652 0.5441541
2      -0.4  -1.09693 0.4387722 0.5272266
3      -0.3  -1.09693 0.3290791 0.5102363
4      -0.2  -1.09693 0.2193861 0.4932223
5      -0.1  -1.09693 0.1096930 0.4762239
6       0.0  -1.09693 0.0000000 0.4592805
Code 
# Add lines for model prediction with three levels of arsenic (5, 50, 95th)
lines(xx$c_dist100[xx$c_arsenic == arsenic[1]], xx$ypred[xx$c_arsenic == arsenic[1]], lty = 1)
lines(xx$c_dist100[xx$c_arsenic == arsenic[2]], xx$ypred[xx$c_arsenic == arsenic[2]], lty = 2)
lines(xx$c_dist100[xx$c_arsenic == arsenic[3]], xx$ypred[xx$c_arsenic == arsenic[3]], lty = 3)

# Add text to plot
ma <- mean(wells$arsenic)
text(x = -1, y = 0.4, labels = paste("As:", round(arsenic[1] + ma, 2)), pos = 4, cex = 0.7)
text(x = -1, y = 0.7, labels = paste("As:", round(arsenic[2] + ma, 2)), pos = 4, cex = 0.7)
text(x = -1, y = 0.95, labels = paste("As:", round(arsenic[3] + ma, 2)), pos = 4, cex = 0.7)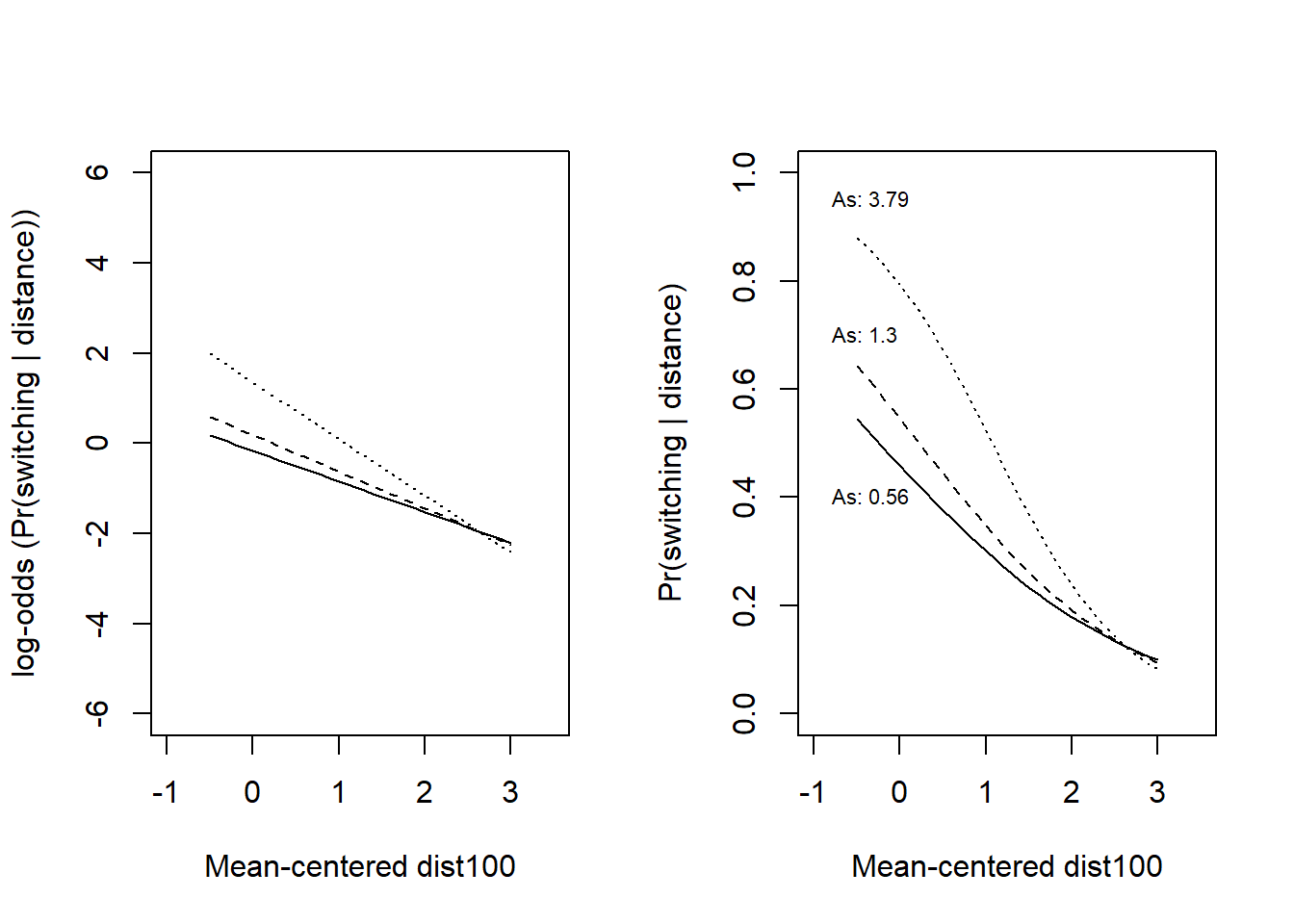


Note that the interaction term is negative, but that its size is uncertain. Below the posterior probability for the interaction, about 4 % above zero, so the 95 % compatibility interval includes zero.

Code 
s5 <- data.frame(fit_5)
colnames(s5) <- c("b0", "dist", "arsenic", "dxa")

plot(density(s5$dxa), main = "Posterior prob. interaction", 
     xlab = "c_dist100:c_arsenic")
abline(v = 0, col = "blue")
text(0.1, 0.7, labels = paste("P(x > 0) = ", round(mean(s5$dxa > 0), 3)), 
     cex = 0.8)
lines(quantile(s5$dxa, prob = c(0.025, 0.975)), c(0.1, 0.1), col = "blue")
points(median(s5$dxa), 0.1, pch = 21, bg = "blue")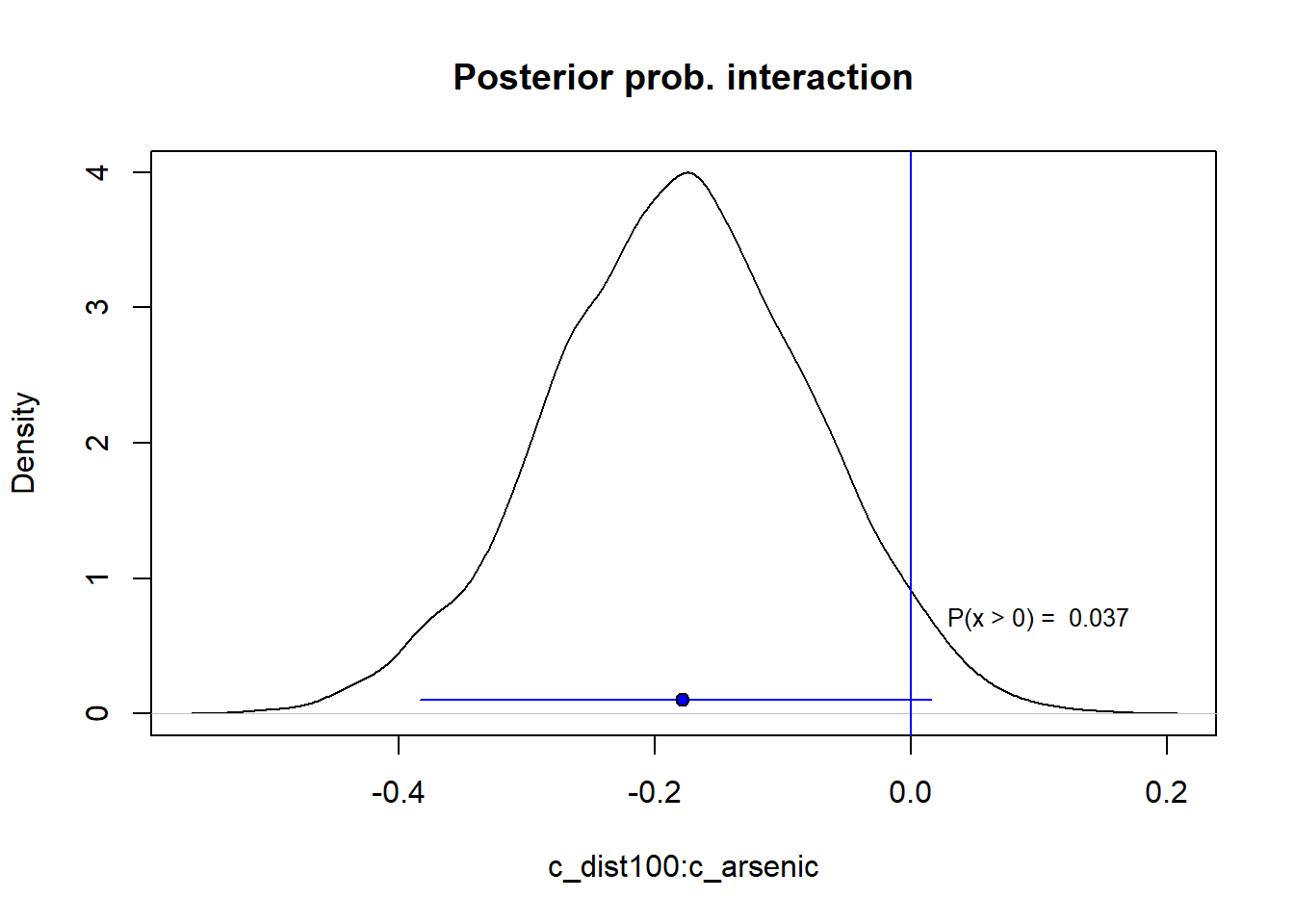

Code 
# Posterior interval
posterior_interval(fit_5, prob = 0.95)
                          2.5%       97.5%
(Intercept)          0.2744100  0.42970803
c_dist100           -1.0821656 -0.67956972
c_arsenic            0.3903326  0.55106241
c_dist100:c_arsenic -0.3837574  0.01596276


Add social predictors

Gelman et al’s model, p. 252.

Code 
wells$c_educ4 <- wells$educ4 - mean(wells$educ4)

fit_8 <- stan_glm(switch ~ c_dist100 + c_arsenic + c_educ4 +
                      c_dist100:c_educ4 + c_arsenic:c_educ4,
                  family = binomial(link="logit"), data = wells, refresh = 0)
print(fit_8)
stan_glm
 family:       binomial [logit]
 formula:      switch ~ c_dist100 + c_arsenic + c_educ4 + c_dist100:c_educ4 + 
       c_arsenic:c_educ4
 observations: 3020
 predictors:   6
------
                  Median MAD_SD
(Intercept)        0.3    0.0  
c_dist100         -0.9    0.1  
c_arsenic          0.5    0.0  
c_educ4            0.2    0.0  
c_dist100:c_educ4  0.3    0.1  
c_arsenic:c_educ4  0.1    0.0  

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg


16.4 Check residuals in logistic regression (optional!)

See Gelman et al. Section 14.5 (pp. 253-256).

Code 
# This function is from Gelman et al. It calculates binned residuals.
# Input: x = fitted values (y-hat) or a predictor variable, y = residuals
binned_resids <- function (x, y, nclass=sqrt(length(x))){
  breaks.index <- floor(length(x)*(1:(nclass-1))/nclass)
  breaks <- c (-Inf, sort(x)[breaks.index], Inf)
  output <- NULL
  xbreaks <- NULL
  x.binned <- as.numeric (cut (x, breaks))
  for (i in 1:nclass){
    items <- (1:length(x))[x.binned==i]
    x.range <- range(x[items])
    xbar <- mean(x[items])
    ybar <- mean(y[items])
    n <- length(items)
    sdev <- sd(y[items])
    output <- rbind (output, c(xbar, ybar, n, x.range, 2*sdev/sqrt(n)))
  }
  colnames (output) <- c ("xbar", "ybar", "n", "x.lo", "x.hi", "2se")
  return (list (binned=output, xbreaks=xbreaks))
}


Plot binned residuals

Code 
pred8 <- fitted(fit_8)
br8 <- binned_resids(pred8, wells$switch-pred8, nclass=40)$binned
plot(range(br8[,1]), range(br8[,2],br8[,6],-br8[,6]),
     xlab="Estimated  Pr (switching)", ylab="Average residual",
     type="n", main="Binned residual plot", mgp=c(2,.5,0), ylim = c(-0.2, 0.2))
abline(0,0, col="gray", lwd=.5)
lines(br8[,1], br8[,6], col="gray", lwd=.5)
lines(br8[,1], -br8[,6], col="gray", lwd=.5)
points(br8[,1], br8[,2], pch=20, cex=.5)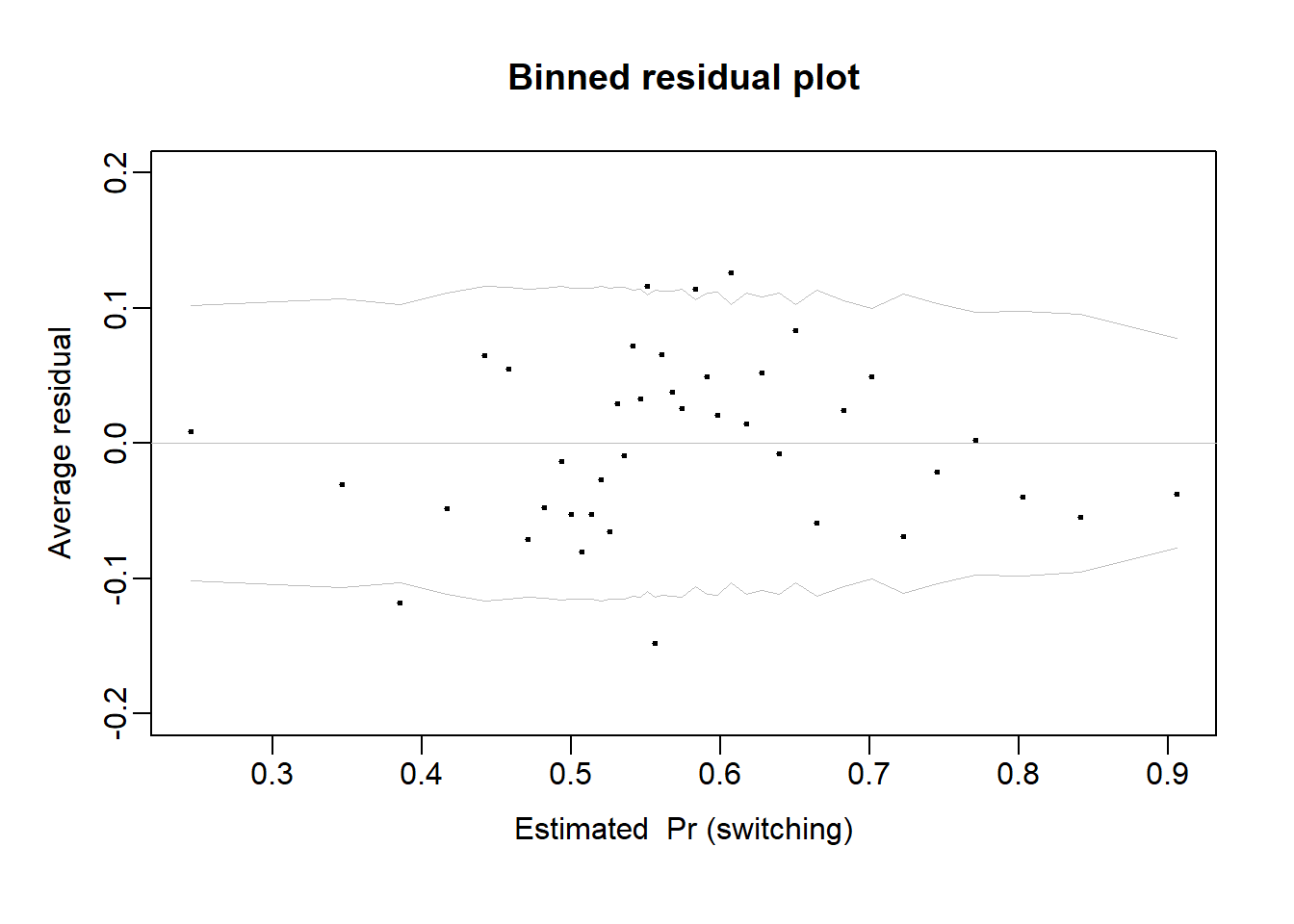

Code 
#lines(lowess(pred8, wells$switch-pred8), col = "red", lty = 3)


Binned residuals with respect to predictors: Distance (left) and Arsenic level (right)

Code 
par(mfrow = c(1, 2))

# Distance
br <- binned_resids(wells$dist, wells$switch-pred8, nclass=40)$binned
plot(range(br[,1]), range(br[,2],br[,6],-br[,6]),
     xlab="Distance to nearest safe well", ylab="Average residual",
     type="n", main="Binned residual plot", mgp=c(2,.5,0), ylim = c(-0.2, 0.2))
abline(0,0, col="gray", lwd=.5)
n_within_bin <- length(wells$switch)/nrow(br)
lines(br[,1], br[,6], col="gray", lwd=.5)
lines(br[,1], -br[,6], col="gray", lwd=.5)
points(br[,1], br[,2], pch=20, cex=.5)
lines(lowess(wells$dist, wells$switch-pred8), col = "red", lty = 3)

#Arsenic
br <- binned_resids(wells$arsenic, wells$switch-pred8, nclass=40)$binned
plot(range(0,br[,1]), range(br[,2],br[,6],-br[,6]),
     xlab="Arsenic level", ylab="Average residual",
     type="n", main="Binned residual plot", mgp=c(2,.5,0), ylim = c(-0.2, 0.2))
abline (0,0, col="gray", lwd=.5)
lines (br[,1], br[,6], col="gray", lwd=.5)
lines (br[,1], -br[,6], col="gray", lwd=.5)
points (br[,1], br[,2], pch=20, cex=.5)
lines(lowess(wells$arsenic, wells$switch-pred8), col = "red", lty = 3)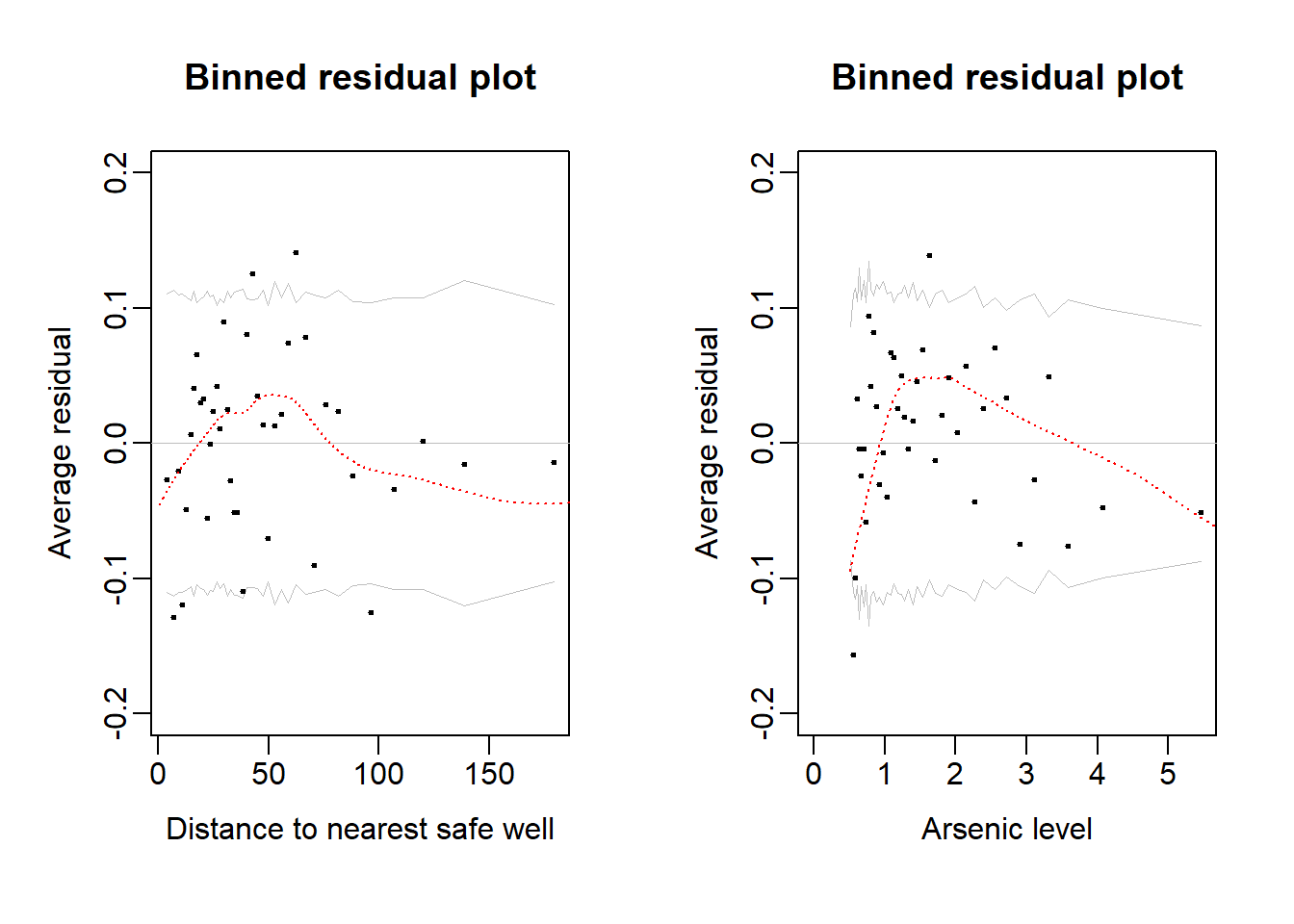


Gelman et al’s final model with log-arsenic, p. 254.

Code 
wells$log_arsenic <- log(wells$arsenic)
wells$c_log_arsenic <- wells$log_arsenic - mean(wells$log_arsenic)

fit_9 <- stan_glm(switch ~ c_dist100 + c_log_arsenic + c_educ4 +
                      c_dist100:c_educ4 + c_log_arsenic:c_educ4,
                  family = binomial(link="logit"), data = wells, refresh = 0)
print(fit_9, digits = 2)
stan_glm
 family:       binomial [logit]
 formula:      switch ~ c_dist100 + c_log_arsenic + c_educ4 + c_dist100:c_educ4 + 
       c_log_arsenic:c_educ4
 observations: 3020
 predictors:   6
------
                      Median MAD_SD
(Intercept)            0.34   0.04 
c_dist100             -1.01   0.11 
c_log_arsenic          0.91   0.07 
c_educ4                0.18   0.04 
c_dist100:c_educ4      0.35   0.11 
c_log_arsenic:c_educ4  0.06   0.07 

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg


Plot the model to understand the distance:education interaction, left on the log-odds scale, right on the probability scale.

Code 
par(mfrow = c(1, 2))

## Plot, with outcome on log-odds scale ----
plot(NULL, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Mean-centered dist100",
     ylab = "log-odds (Pr(switching | distance))", 
     xlim = c(-1, 3.5), ylim = c(-6, 6))

# Model predictions, in data-frame called xx
cf <- coef(fit_9)
x <- seq(from = -0.5, to = 3, by = 0.1)
edu <- quantile(wells$c_educ4, c(0.05, 0.5, 0.95))
xx <- expand.grid(c_dist100 = x, c_educ4 = edu)
xx$dxe <- xx$c_dist100*xx$c_educ4
# At arsenic = 0, so cf[3] and cf[5] are gone
xx$ypred <- cf[1] + cf[2]*xx$c_dist100 + cf[4]*xx$c_educ4 + cf[5]*xx$dxe
head(xx)
  c_dist100   c_educ4       dxe     ypred
1      -0.5 -1.207119 0.6035596 0.8293254
2      -0.4 -1.207119 0.4828477 0.6869369
3      -0.3 -1.207119 0.3621358 0.5445483
4      -0.2 -1.207119 0.2414238 0.4021598
5      -0.1 -1.207119 0.1207119 0.2597712
6       0.0 -1.207119 0.0000000 0.1173826
Code 
# Add lines for model prediction with three levels of education (5, 50, 95th)
lines(xx$c_dist100[xx$c_educ4 == edu[1]], xx$ypred[xx$c_educ4 == edu[1]], lty = 1)
lines(xx$c_dist100[xx$c_educ4 == edu[2]], xx$ypred[xx$c_educ4 == edu[2]], lty = 2)
lines(xx$c_dist100[xx$c_educ4 == edu[3]], xx$ypred[xx$c_educ4 == edu[3]], lty = 3)

# Add text to plot
#text(x = -1, y = 0, labels = paste("As:", round(arsenic[1], 2)), pos = 4, cex = 0.8)
#text(x = -1, y = 0.7, labels = paste("As:", round(arsenic[2], 2)), pos = 4, cex = 0.8)
#text(x = -1, y = 2.2, labels = paste("As:", round(arsenic[3], 2)), pos = 4, cex = 0.8)


## Plot data, probability scale see Fig. 13.10 (left) in Gelman et al. ----
plot(NULL, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Mean-centered dist100",
     ylab = "Pr(switching | distance)", 
     xlim = c(-1, 3.5), ylim = c(0, 1))

# Model predictions, in data-frame called xx
cf <- coef(fit_9)
x <- seq(from = -0.5, to = 3, by = 0.1)
edu <- quantile(wells$c_educ4, c(0.05, 0.5, 0.95))
xx <- expand.grid(c_dist100 = x, c_educ4 = edu)
xx$dxe <- xx$c_dist100*xx$c_educ4
# At arsenic = 0, so cf[3] and cf[5] are gone
xx$ypred <- plogis(cf[1] + cf[2]*xx$c_dist100 + cf[4]*xx$c_educ4 + cf[5]*xx$dxe)
head(xx)
  c_dist100   c_educ4       dxe     ypred
1      -0.5 -1.207119 0.6035596 0.6962123
2      -0.4 -1.207119 0.4828477 0.6652852
3      -0.3 -1.207119 0.3621358 0.6328698
4      -0.2 -1.207119 0.2414238 0.5992065
5      -0.1 -1.207119 0.1207119 0.5645800
6       0.0 -1.207119 0.0000000 0.5293120
Code 
# Add lines for model prediction with three levels of education (5, 50, 95th)
lines(xx$c_dist100[xx$c_educ4 == edu[1]], xx$ypred[xx$c_educ4 == edu[1]], lty = 1)
lines(xx$c_dist100[xx$c_educ4 == edu[2]], xx$ypred[xx$c_educ4 == edu[2]], lty = 2)
lines(xx$c_dist100[xx$c_educ4 == edu[3]], xx$ypred[xx$c_educ4 == edu[3]], lty = 3)

# Add text to plot
me <- mean(wells$educ)
text(x = 1, y = 0.02, labels = paste("Edu:", round(edu[1] + me, 1), "y"), pos = 4, cex = 0.8)
text(x = 1, y = 0.4, labels = paste("Edu:", round(edu[2] + me, 1), "y"), pos = 4, cex = 0.8)
text(x = 1, y = 0.6, labels = paste("Edu:", round(edu[3] + me, 1), "y"), pos = 4, cex = 0.8)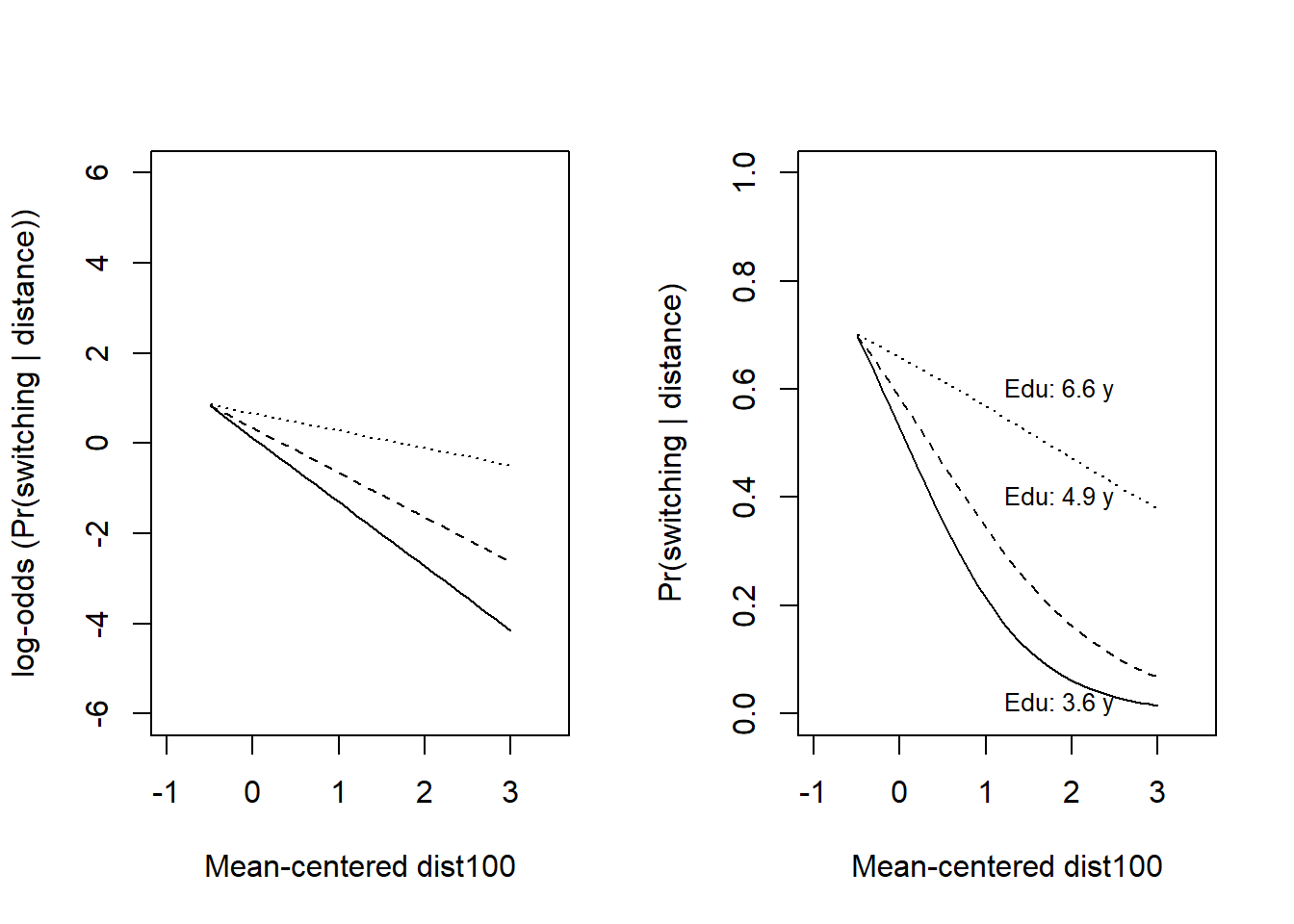


Code 
s9 <- data.frame(fit_9)
plot(density(s9$c_dist100.c_educ4), main = "DistxEdu interaction", 
     xlab = "c_dist100:c_educ4")
abline(v = 0, col = "blue")
lines(quantile(s9$c_dist100.c_educ4, prob = c(0.025, 0.975)), c(0.1, 0.1), col = "blue")
points(median(s9$c_dist100.c_educ4), 0.1, pch = 21, bg = "blue")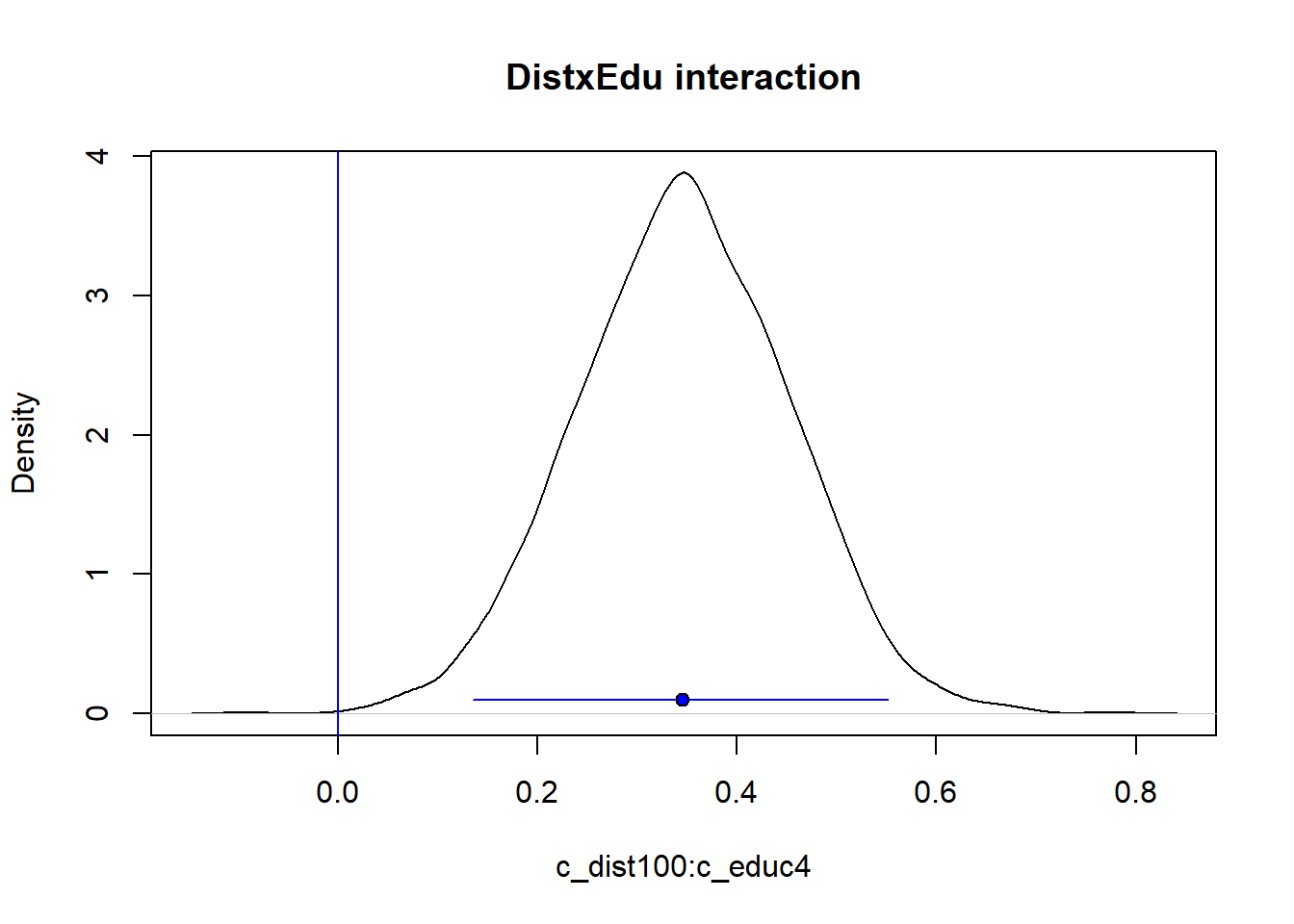


Practice

The practice problems are labeled Easy (E), Medium (M), and Hard (H), (as in McElreath (2020)).

Easy

16E1.

  1. When is it safe to interpret the odds ratio (OR) as a relative risk (RR).

  2. Is it always the case that OR > RR?


16E2.

Which of the following statements about logistic regression are true?

Select one or more alternatives:

  • Assume that residuals are normally distributed

  • Estimates probabilities

  • Has higher power than linear regression

  • Can only be used with multiple predictors

  • Is defined for outcomes in the interval [-1, 1]

  • Involve a logit link function

  • Used to model binary outcomes

  • Can be used to fit an intercept only model to estimate a single proportion

  • The exponentiated intercept, \(exp(b_0)\) can be interpreted as an odds ratio

  • Regression coefficients (“slopes”) divided by 4, \(b_1/4\), can be interpreted as an upper limit to the probability difference associated with a one-unit difference in the predictor


Medium

16M1. Make sense of this: “In logistic regression variables are interacting with them selves: The effect of a variable X on the probability of outcome depends on the level of X!”


16M2. Figure below is from the Bangladesh well-switching data discussed above.

  1. Estimate by eye the predicted difference in probability of switching wells between people living 200 m compared to 0 m (next to) the nearest safe well.

  2. Estimate by eye the odds ratio for the same comparison, between people living 200 compared to 0 m from the nearest well.

Code 
# function to jitter data points
jitter_binary <- function(a, jitt = 0.05){
  ifelse(a == 0, runif(length(a), 0, jitt), runif(length(a), 1- jitt, 1))
}

wells$switch_jitter <- jitter_binary(wells$switch)

# Plot jittered data
plot(wells$dist100, wells$switch_jitter, pch = 16, col = rgb(0, 0, 1, 0.1), 
     xlab = "Distance (in 100-m) to nearest safe well",
     ylab = "Pr(switching | distance)")
cf <- coef(fit_1)
x <- seq(from = 0, to = 4, by = 0.1)
ypred <- plogis(cf[1] + cf[2]*x)
lines(x, ypred)

# Grid lines
for (j in seq(0, 3.5, 0.25)) { lines(c(j, j), c(0, 1), lty =2, col = "grey")}
for (j in seq(0, 1.0, 0.1)) { lines(c(0, 3.5), c(j, j), lty =2, col = "grey")}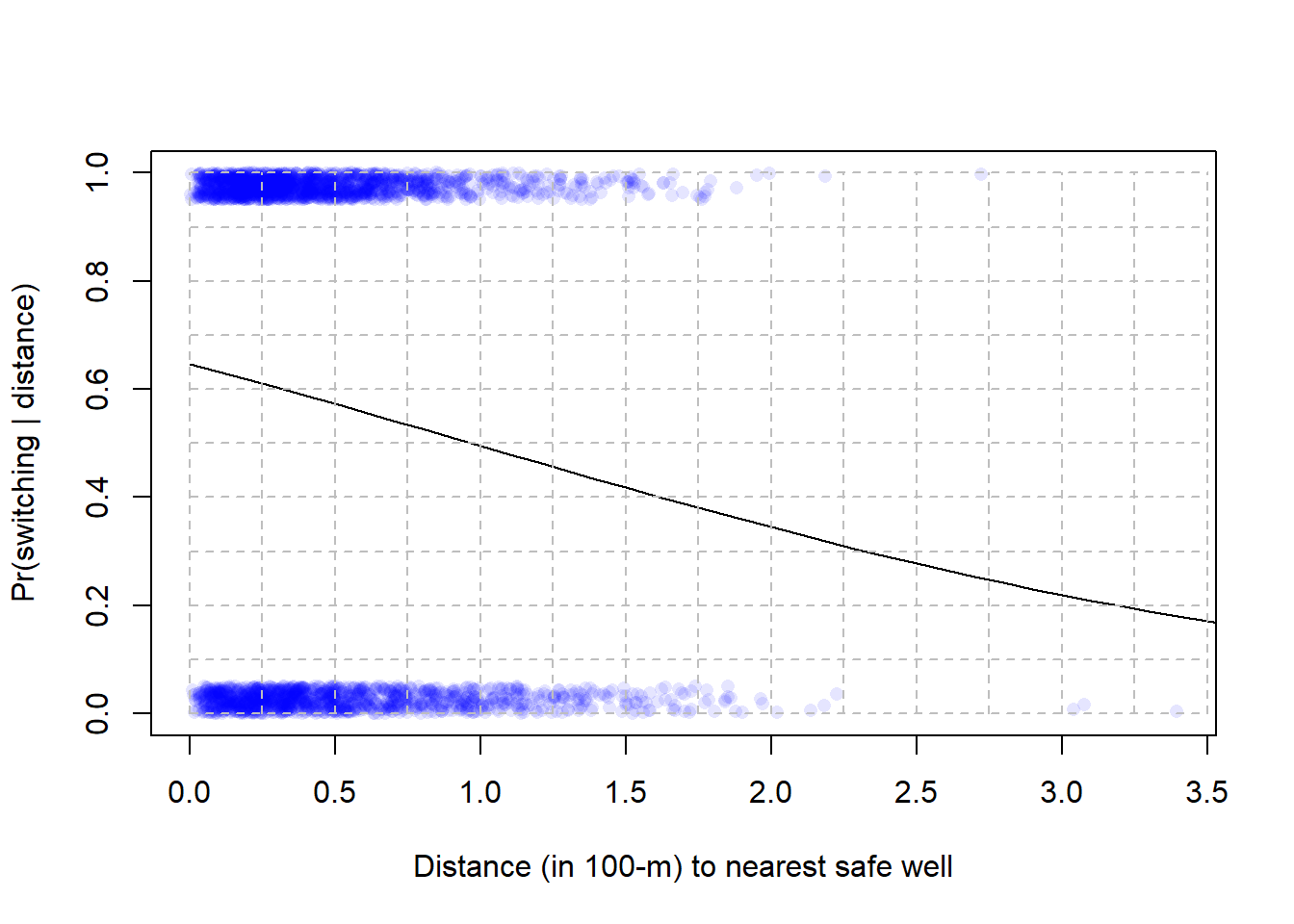


16M3. Below regression estimate for the model displayed in 16M2. Use the coefficients to calculate answers to 16M2

Code 
print(fit_1, digits = 2)
stan_glm
 family:       binomial [logit]
 formula:      switch ~ dist100
 observations: 3020
 predictors:   2
------
            Median MAD_SD
(Intercept)  0.61   0.06 
dist100     -0.62   0.09 

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg


Hard

16H1. Revisit the well-switching data discussed above. Fit a model predicting well-switching from distance and arsenic-level as well as their interaction. Visualize and interpret the result.


(Session Info)

Code 
sessionInfo()
R version 4.4.2 (2024-10-31 ucrt)
Platform: x86_64-w64-mingw32/x64
Running under: Windows 11 x64 (build 26100)

Matrix products: default


locale:
[1] LC_COLLATE=Swedish_Sweden.utf8  LC_CTYPE=Swedish_Sweden.utf8   
[3] LC_MONETARY=Swedish_Sweden.utf8 LC_NUMERIC=C                   
[5] LC_TIME=Swedish_Sweden.utf8    

time zone: Europe/Stockholm
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] rstanarm_2.32.1 Rcpp_1.0.14    

loaded via a namespace (and not attached):
 [1] tidyselect_1.2.1     dplyr_1.1.4          farver_2.1.2        
 [4] loo_2.8.0            fastmap_1.2.0        tensorA_0.36.2.1    
 [7] shinystan_2.6.0      promises_1.3.3       shinyjs_2.1.0       
[10] digest_0.6.37        mime_0.13            lifecycle_1.0.4     
[13] StanHeaders_2.32.10  survival_3.7-0       magrittr_2.0.3      
[16] posterior_1.6.1      compiler_4.4.2       rlang_1.1.6         
[19] tools_4.4.2          igraph_2.1.4         yaml_2.3.10         
[22] knitr_1.50           htmlwidgets_1.6.4    pkgbuild_1.4.8      
[25] curl_6.4.0           plyr_1.8.9           RColorBrewer_1.1-3  
[28] dygraphs_1.1.1.6     abind_1.4-8          miniUI_0.1.2        
[31] grid_4.4.2           stats4_4.4.2         xts_0.14.1          
[34] xtable_1.8-4         inline_0.3.21        ggplot2_3.5.2       
[37] scales_1.4.0         gtools_3.9.5         MASS_7.3-61         
[40] cli_3.6.5            rmarkdown_2.29       reformulas_0.4.1    
[43] generics_0.1.4       RcppParallel_5.1.10  rstudioapi_0.17.1   
[46] reshape2_1.4.4       minqa_1.2.8          rstan_2.32.7        
[49] stringr_1.5.1        shinythemes_1.2.0    splines_4.4.2       
[52] bayesplot_1.13.0     parallel_4.4.2       matrixStats_1.5.0   
[55] base64enc_0.1-3      vctrs_0.6.5          V8_6.0.4            
[58] boot_1.3-31          Matrix_1.7-1         jsonlite_2.0.0      
[61] crosstalk_1.2.1      glue_1.8.0           nloptr_2.2.1        
[64] codetools_0.2-20     distributional_0.5.0 DT_0.33             
[67] stringi_1.8.7        gtable_0.3.6         later_1.4.2         
[70] QuickJSR_1.8.0       lme4_1.1-37          tibble_3.3.0        
[73] colourpicker_1.3.0   pillar_1.10.2        htmltools_0.5.8.1   
[76] R6_2.6.1             Rdpack_2.6.4         evaluate_1.0.3      
[79] shiny_1.11.1         lattice_0.22-6       markdown_2.0        
[82] rbibutils_2.3        backports_1.5.0      threejs_0.3.4       
[85] httpuv_1.6.16        rstantools_2.4.0     gridExtra_2.3       
[88] nlme_3.1-166         checkmate_2.3.2      xfun_0.52           
[91] zoo_1.8-14           pkgconfig_2.0.3