4  S: Descriptive Statistics and Visualization

Load R-libraries

# Only base-R used in this chapter!

Topics

• Central tendency (location)
  • Mean
  • Median
• Dispersion (scale)
  • Standard deviation
  • Median absolute deviation (MAD)
  • Inter Quartile Range (IQR)
• Quantiles
  • Quartiles
  • Percentiles
• Exploratory visualizations. Displaying raw data to see things that you may otherwise miss. Three types of plots described below. When used for exploratory analysis, they don’t have to look pretty as they are not intended for publication (cf. Gelman et al., 2021, p. 30).
  • Boxplot
  • Histogram
  • Kernel density plot
  • Profile plot
• Transformations
  • Linear transformations, for example, reversing, centering and z-scores
  • Non-linear transformations, for example, the log-transform
• Probability (continued form ch 2)
  • Binomial distribution, \(Binom(n, p)\)
  • Probability versus density
  • Normal distribution, \(Normal(\mu, \sigma)\)
    • Probability Density Function (PDF), in R: dnorm()
    • Cumulative Distribution Function (CDF), in R: pnorm()
    • Standard Normal: \(Normal(\mu = 0, \sigma = 1)\)

Readings.

Gelman et al. (2021) do not cover basic descriptive statistics. But read chapter 2 on data visualization in general, there are many good points that we may come back to. Sections 3.3-3.4 are helpful if you are rusty on linear relationships and logarithms. We will get back to transformations in the chapters on regression. But if you want to jump ahead, please read sections 12.1-12.5 in chapter 12. For probability distributions, see Chapter 3, Section 3.5.

4.1 Descriptive statistics

Central tendency

• Mean. Assumes at least interval-scale data. The mean is efficient for well-behaved data, but not robust to outliers. May be harder to interpret than the median, as the mean value can be representative or unrepresentative of a typical observation.
• Median. Can be used for rank-order-scale data. Easy to interpret, it is the middle value, half of the observations are below and half above the median (assuming no ties). It is less efficient for well-behaved data than the mean, but may be more efficient than the mean for non-normal data, and it is robust to outliers.

Dispersion

• Standard deviation, often reported together with the mean. Like the mean, the standard deviation is sensitive to outliers.
• Inter-quartile range (IQR), often reported together with the median, give the range of the middle 50 % of the data (see below, quantiles).
• Median absolute deviation (MAD), often reported together with the median. Note that the MAD typically is multiplied by a constant = 1.4826 to make the expected value of MAD for a normal distribution equal to its standard deviation, \(\sigma\).

Quantiles

Quantiles are cut-off points dividing the data in parts, A quantile define how large proportion of the data that is below (or above) a given cut-off. Two types of quantiles are:

• percentiles. Divides the data in 100 parts. The 10th percentile give the value below which 10 % of the data is located, the 50th percentile give the value below which half of the data is located (i.e., the median), etc.
• quartiles. Divides the data in four quartiles: 25, 50 and 75 % of the data is located below the first, second and third quartile, respectively. These quartiles are represented by the vertical lines of the box in a boxplot (see below).

4.2 Visualization

Histogram

Histograms visualize a frequency distribution with rectangles representing the number (or proportion) of observations in intervals of the same size. Useful to get a feeling for the the shape of a distribution of values. Here a simple example using simulated data:

n <- 1000  

# Simulate data by random draws from a skewed distribution (Gamma) 
x <- round(100 * rgamma(100, 3, 3))  

par(mfrow = c(1, 2))  # Two plots next to each other

# Histogram with 50-unit bins (<50, 50-99, 100-149, ...)
hist(x, breaks = seq(0, 500, by = 50), main = "Bin size = 50")

# Histogram with 10-unit bins (<50, 50-99, 100-149, ...)
hist(x, breaks = seq(0, 500, by = 10), main = "Bin size = 10")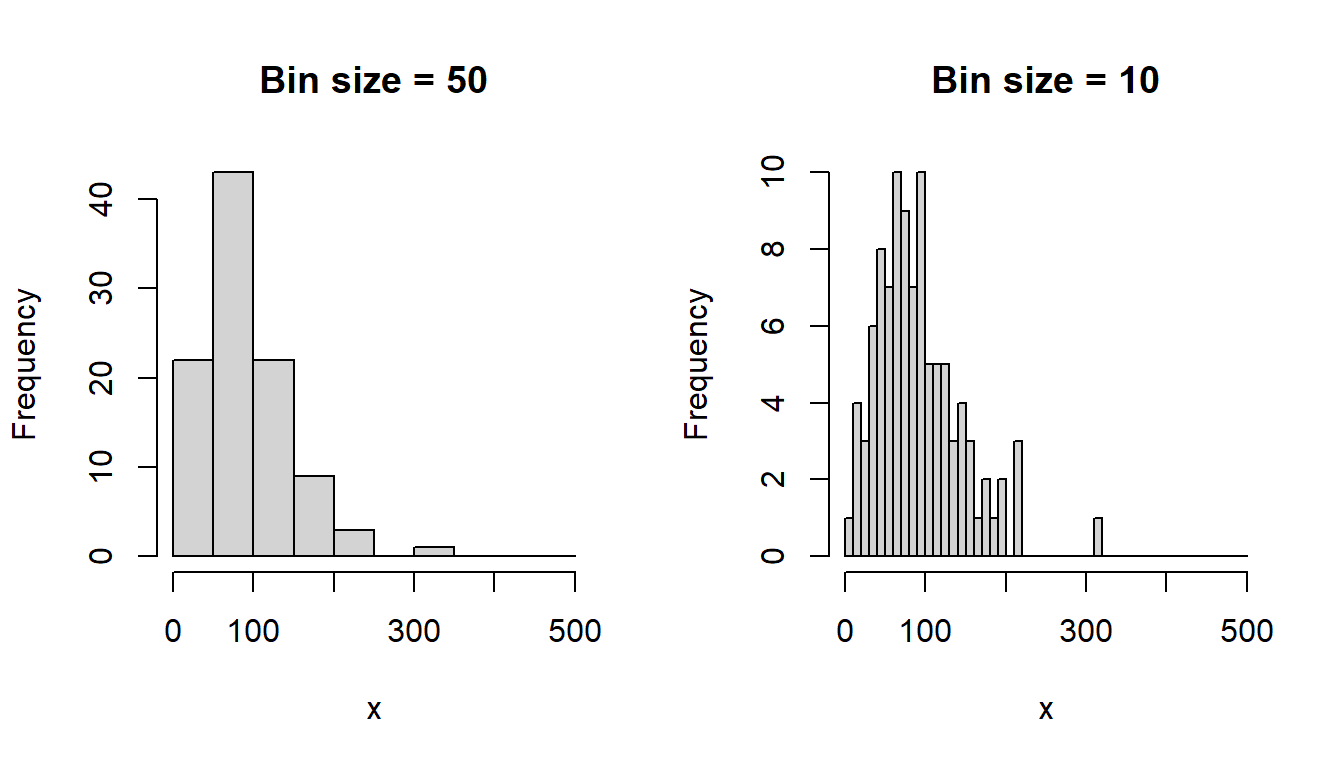

Kernel density plot

The shape of a histogram depends on the analysts choice of bin size (see figure above). Kernel density plots are less dependent on such choices. (Example taken from chapter 2 of Howell, 2012)

Here’s the general principle:

# Some observations
x <- c(0.0, 1.0, 1.1, 1.5, 1.9, 2.8, 2.9, 3.5)
x

[1] 0.0 1.0 1.1 1.5 1.9 2.8 2.9 3.5

# Set "error"
ss <- 0.5 # standard deviation of normal

# Plot normal distributions around observed values (+/- error)
xvalues <- seq(-3, 6, by = 0.1)
z <- numeric(length(xvalues))

plot(xvalues, z, ylim = c(0, 2.7), pch = "", xlab = "x", 
     ylab = "density")

z1 <- z # Empty vetcor to start with, and then loop over vector x
for (j in 1:length(x)){
  zout <- dnorm(xvalues, mean = x[j], sd = ss)
  lines(xvalues, zout, col = "black")
  z1 <- z1 + zout
}

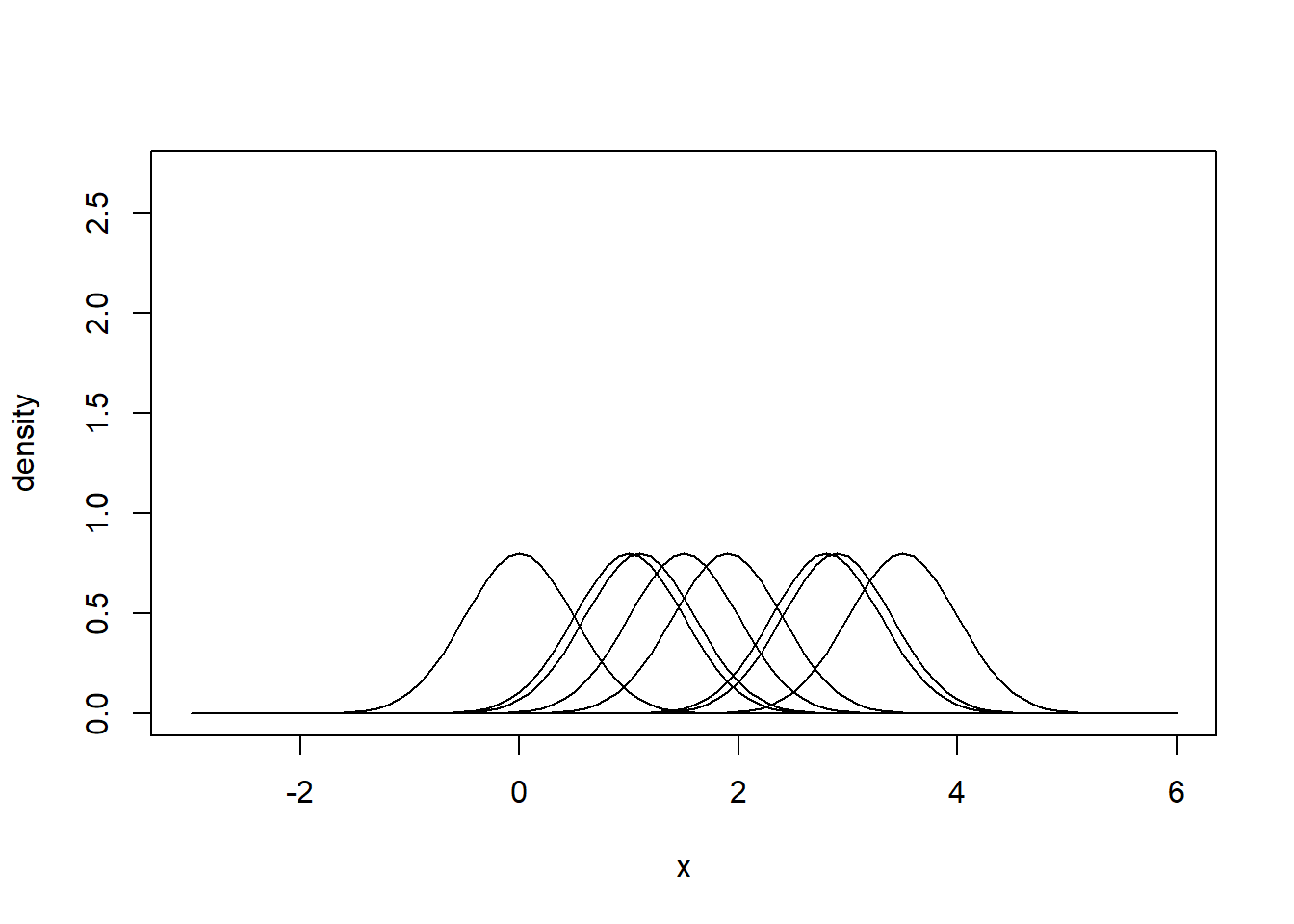
# Sum densities vertically to obtain your kernel density estimator.
# It is an estimator of the true probability density function (PDF) of 
# the population from which the data was sampled.
plot(xvalues, z, ylim = c(0, 2.7), pch = "", xlab = "x", 
     ylab = "density")
lines(xvalues, z1, col = "black")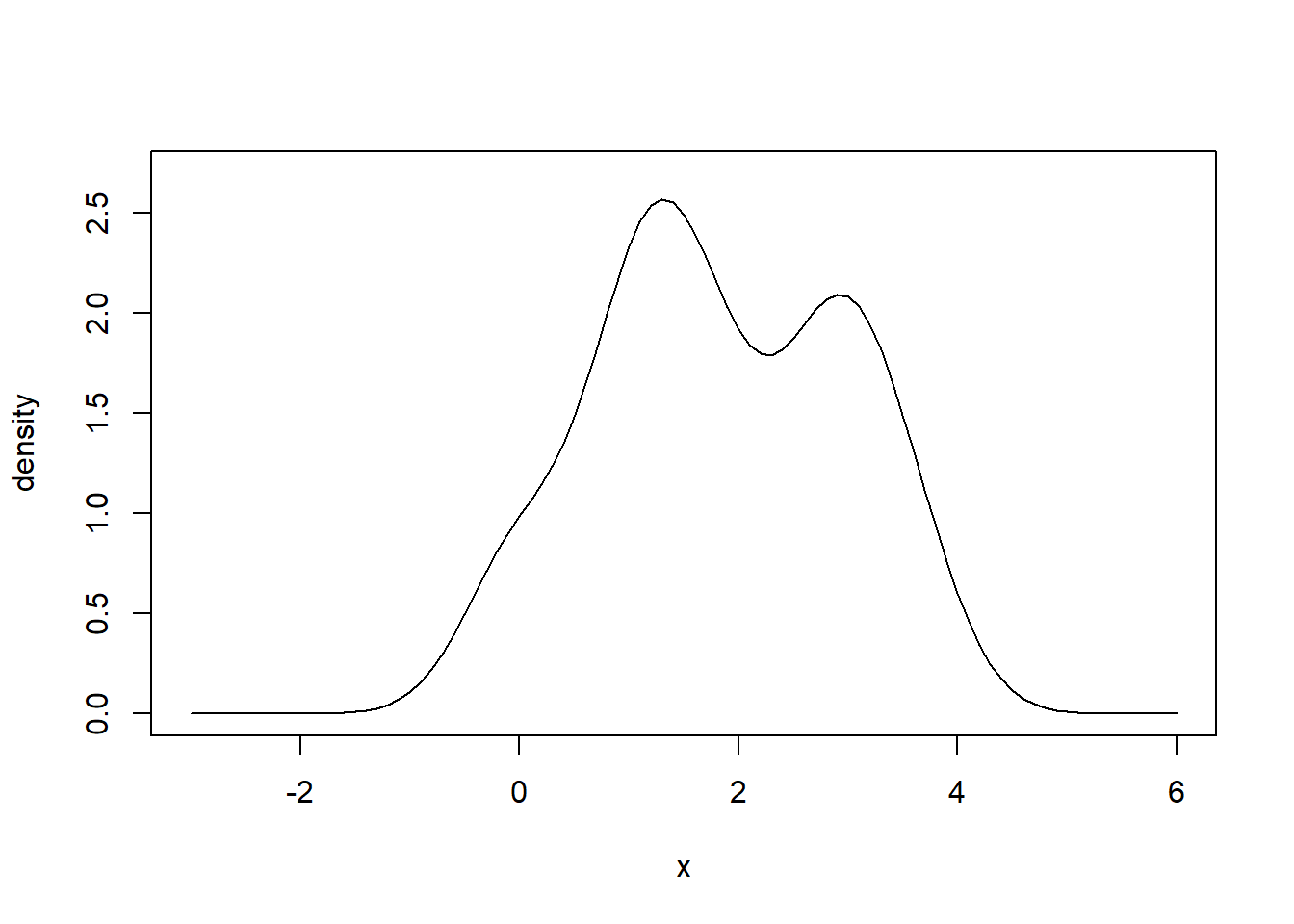

Boxplot

Useful for illustrating the distributions of data. The three horizontal lines of the box show the 75th, 50th (median) and 25th percentiles. Thus, the length of the vertical side of the box is equal to the inter-quartile range (IQR). Data points located more than 1.5 IQR above or below the box are considered outliers and are indicated with symbols. The bottom and top horizontal lines of the figure indicate minimum and maximum value, once outliers have been removed.

set.seed(888)
x <- rt(100, df = 4)  # Random numbers from the T-distribution with df = 4
boxplot(x)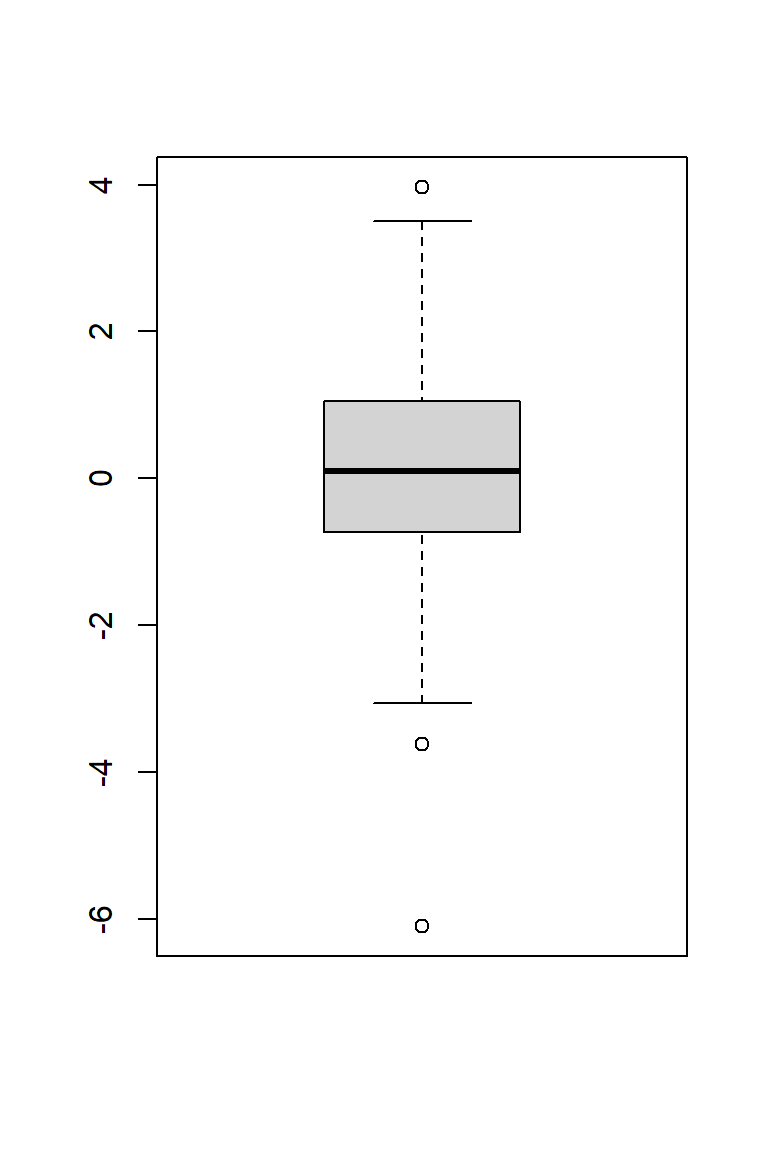

Profile plot

For within-subject data, displaying individual response profiles for each participant can be informative. Below is an example using simulated data from an experiment with 12 participants, each tested under three conditions: A, B, and C.

Simulate data.

# This is a bit advanced, using the multivariate normal to simulate 
# varying effect
set.seed(123)

# Experimental setup
n <- 12  # Number of participants
cond <- rep(c("A", "B", "C"), times = n)  # Experimental conditions
 
# True (unobserved) values for each participant condition
library(MASS)  # for mvrnorm
Mu <- c(50, 60, 55)  # Population mean
s <- 5  # Population sigma of varying effects, assumed the same for all conditions
cv <- s*s*0.7  # Covariance between mu
Sigma <- matrix(c(s^2, cv, cv,   # Covariance matrix
                  cv, s^2, cv,
                  cv, cv,  s^2), nrow = 3, ncol = 3, byrow = TRUE)
truemean <- mvrnorm(n, Mu, Sigma)  # Multivariate random number generator

# Observed values
ss <- 3  # SD within subject
obs <- t(apply(truemean, 1, function(x) rnorm(3, mean = x, sd = ss)))
obs <- cbind(1:12, obs)
colnames(obs) <- c("id", "A", "B", "C")
obs <- data.frame(obs)

Draw profile plot

# Trick to set limits of y-scale to even 5s
ymin <- floor(min(obs[, 2:4])/5)*5
ymax <- ceiling(max(obs[, 2:4])/5)*5

# Empty plot
plot(1:3, 1:3, pch = "", xlab = "Experimental condition",
     ylab = "Outcome", axes = FALSE, xlim = c(0.5, 3.5), ylim = c(ymin, ymax))

# Draw profiles for each id using a for-loop
for (j in obs$id){
  idd <- obs[obs$id == j, ]
  lines(1:3, idd[, 2:4], lty = 1, col = "grey")
  points(1:3, idd[, 2:4], pch = 21, bg = "grey")
  
}

# Add axis
axis(1, at = c(0.5, 1, 2, 3, 3.5), labels = c("", "A", "B", "C", ""), pos = ymin)
axis(2, at = seq(ymin, ymax, 5), pos = 0.5, las = 2)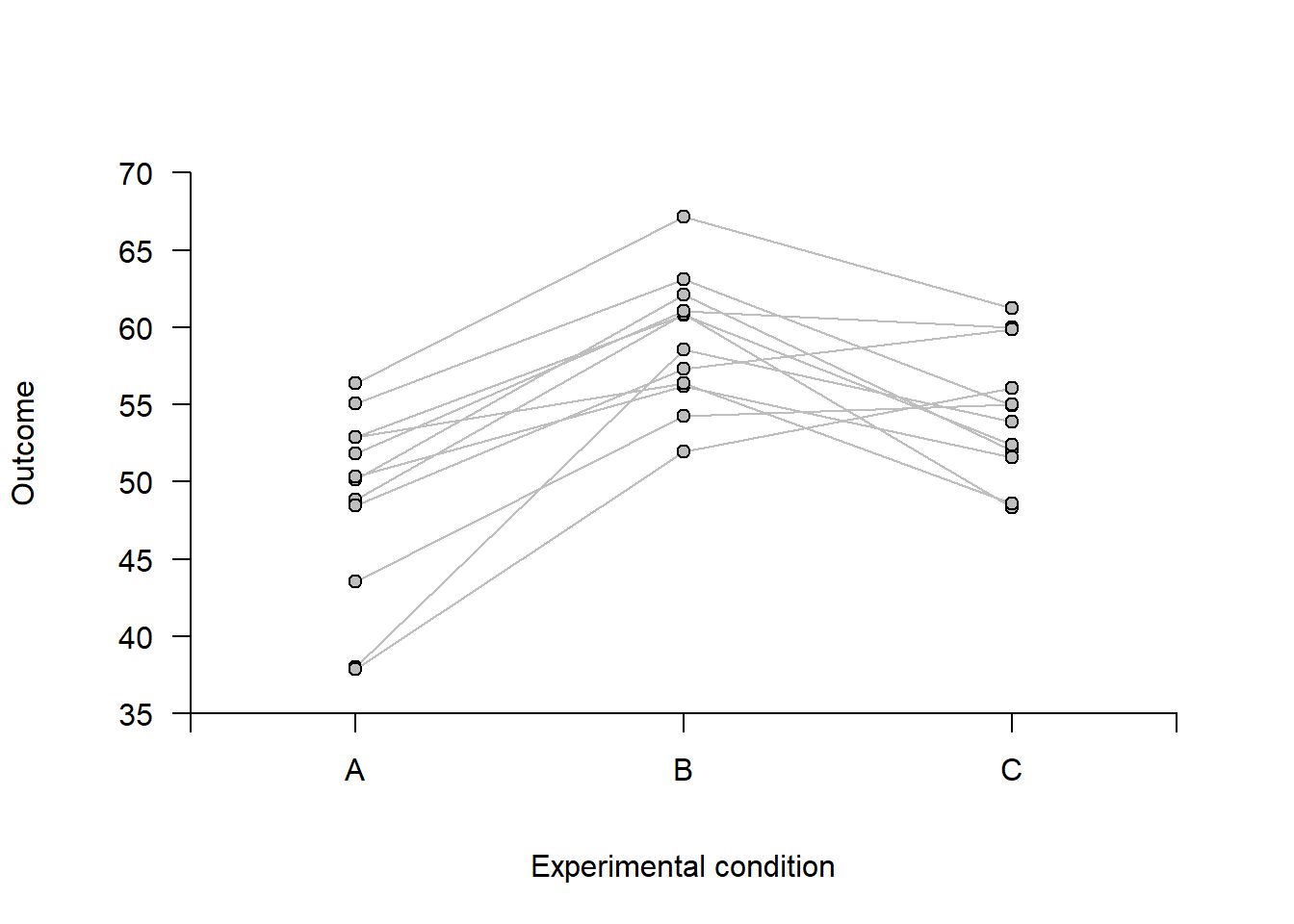

Example data set: rt_howell.txt

Data from Table 2.1 in Howell (2012). (see also analysis that we did in 2: Data Management and Screening).

The data is from a reaction-time experiment with one participant (Howell). The participant was first presented with a list of digits for a few seconds, e.g.,

1, 5, 7

After the list had been removed, Howell was shown a single digit, e.g.,

2

and was asked to determine whether the single digit was on the previously shown list (in the example above, correct answer would be No).

Code book:

• trial – Trial number, from 1 to 300 (here ordered according to stimulus condition, but I presume that stimuli were presented in random orders)
• nstim – Number of digits on the list (1, 3, or 5), we expect longer reaction times for longer lists
• yesno – Whether the single digit asked for was on the list (1, correct answer “Yes”) or not (2, correct answer “No”).
• rt – Reaction time in milliseconds

Note that the data only contain trials in which the answer given was correct,

You may download the data file “rt_howell.txt” from Athena or find the data on my Bitbucket repository.

Follow this link to find data Save (Ctrl+S on a pc) to download as text file

Import data

Once you have downloaded the file and made sure it is in the same folder as your current R-session (you may have done this already last time). To check from where R is working, run getwd() in the Console. Use setwd(dir) to change the directory of the current session, where dir is a character string. Example setwd("C:/Users/MATNI/Documents/Stat1/datafiles") would set R to work in the folder datafiles on my computer.

# Import data.  Note that I have chosen to store the data in a subfolder called 
# "datasets"" located in the directory from which R is working)
d <- read.table("datasets/rt_howell.txt", header = TRUE, sep = ",")

Histogram and Kernel density plots

From last time: Use box plots to inspect data

# Boxplot (there are many ways to make nicer boxplots)

par(mfrow = c(1, 2))  # Two plots next to each other

# Reaction time, all data
boxplot(d$rt, xlab = "All trials", ylab = "Reaction time (ms)")

# Reaction time, per condition
boxplot(d$rt ~ d$yesno + d$nstim, col = c('green', 'red'),
        xlab = "Stimulus condition", ylab = "Reaction time (ms)")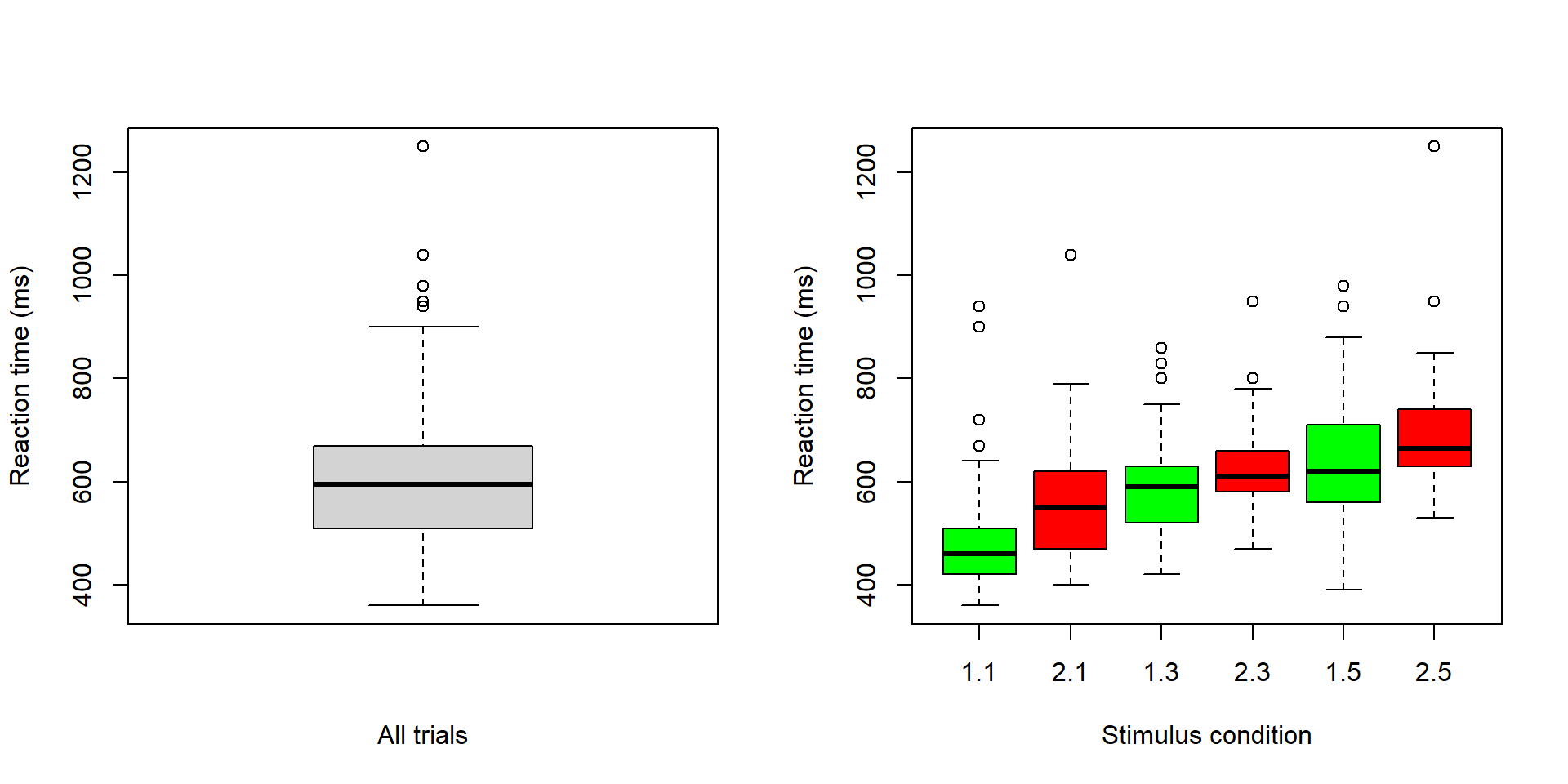

Here a look specifically at the two stimulus conditions with the longest list (condition 1.5, and 2.5 in the boxplot above)

To simplify the following, this code make a reduced data frame g with only the longest-list conditions.

g <- d[d$nstim == 5, ]  # Reduce data frame to simplify the following work

Histogram and density plot overlays for the “Yes” trials.

# Histogram for yes trials
hist(g$rt[g$yesno == 1], breaks = seq(275, 1400, by = 20), 
     freq = TRUE, main = '5-item list, Yes-trials', xlab = "Reaction time (ms)")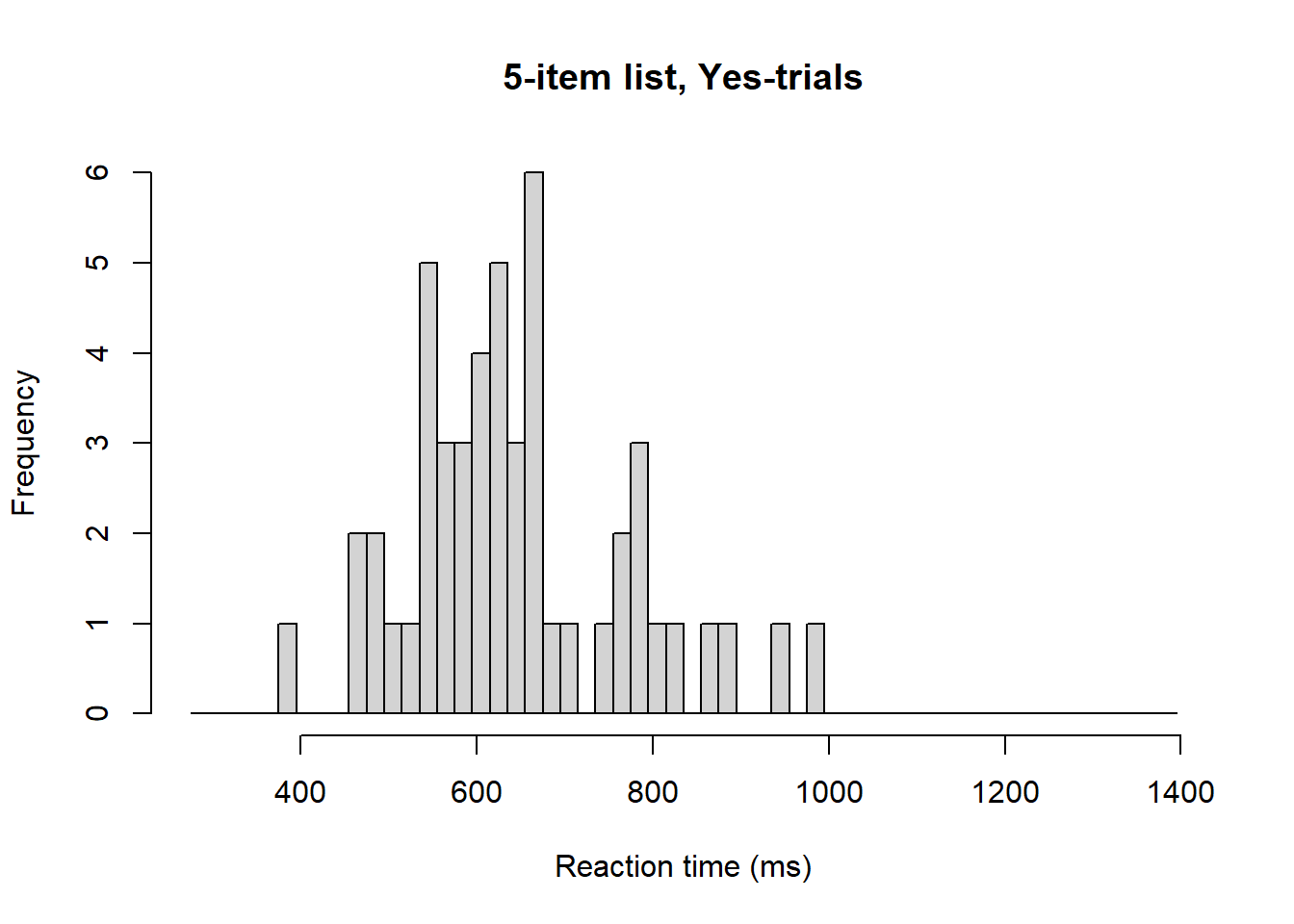

# Same histogram, but note y-axis and argument freq = FALSE
hist(g$rt[g$yesno == 1], breaks = seq(275, 1400, by = 20), 
     freq = FALSE, main = '', xlab = "Reaction time (ms)")

# Add density for yes trials
dens_yes <- density(g$rt[g$yesno == 1])
polygon(dens_yes, col = rgb(0, 1, 0, 0.5))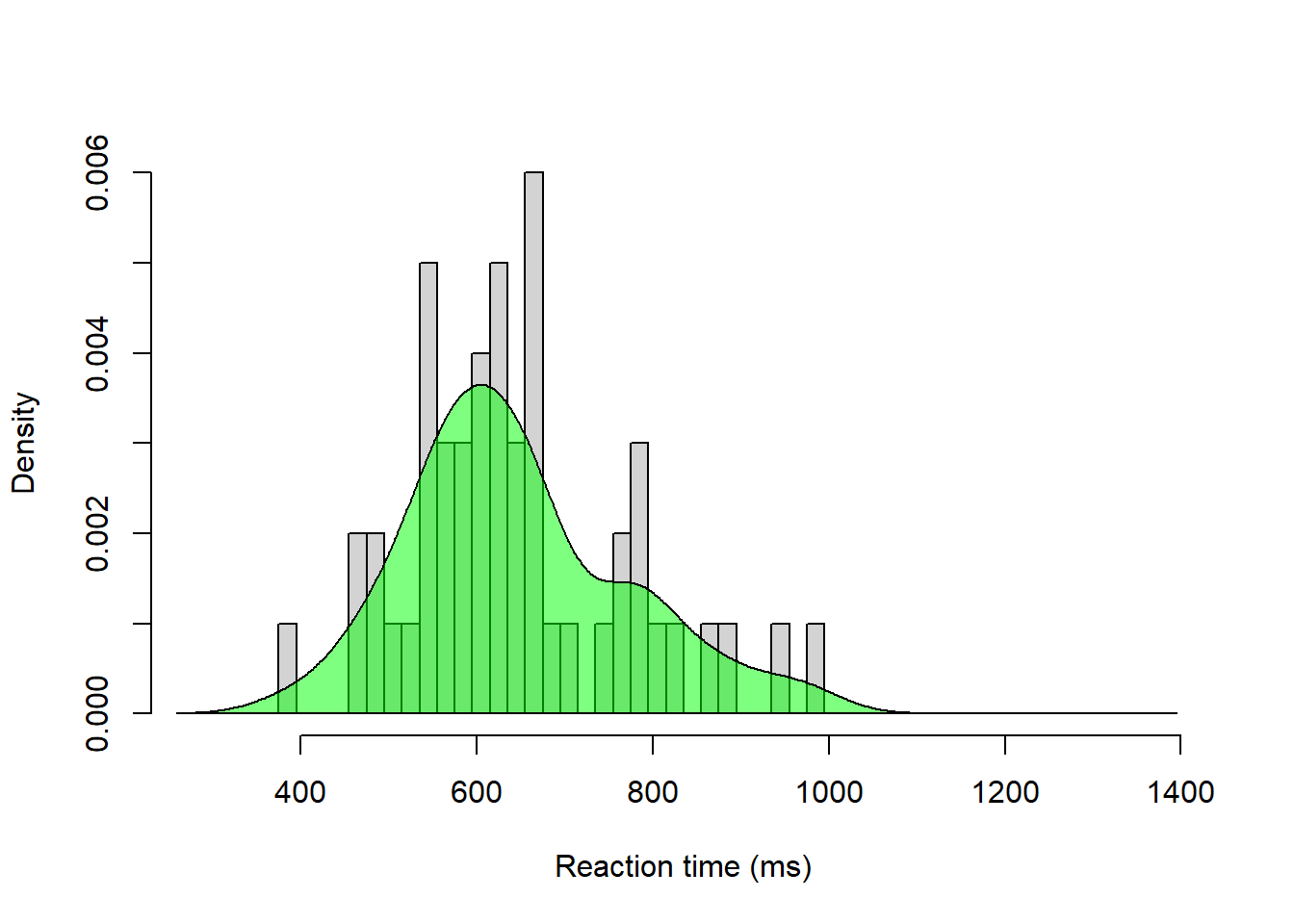

Histogram overlays for “Yes” and “No” trials

# Blank histogram (note argument lty = 'blank', col = "white" to make bars
# invisible)
hist(g$rt, breaks = seq(275, 1400, by = 20), lty = 'blank', col = "White",
     main = '', xlab = "Reaction time (ms)")

# Add histogram for Yes trials
hist(g$rt[g$yesno == 1], breaks = seq(275, 1400, by = 20),
     add = TRUE, col = rgb(0, 1, 0, 0.5))

# Add histogram for No trials
hist(g$rt[g$yesno == 2], breaks = seq(275, 1400, by = 20),
     add = TRUE, col = rgb(1, 0, 0, 0.5))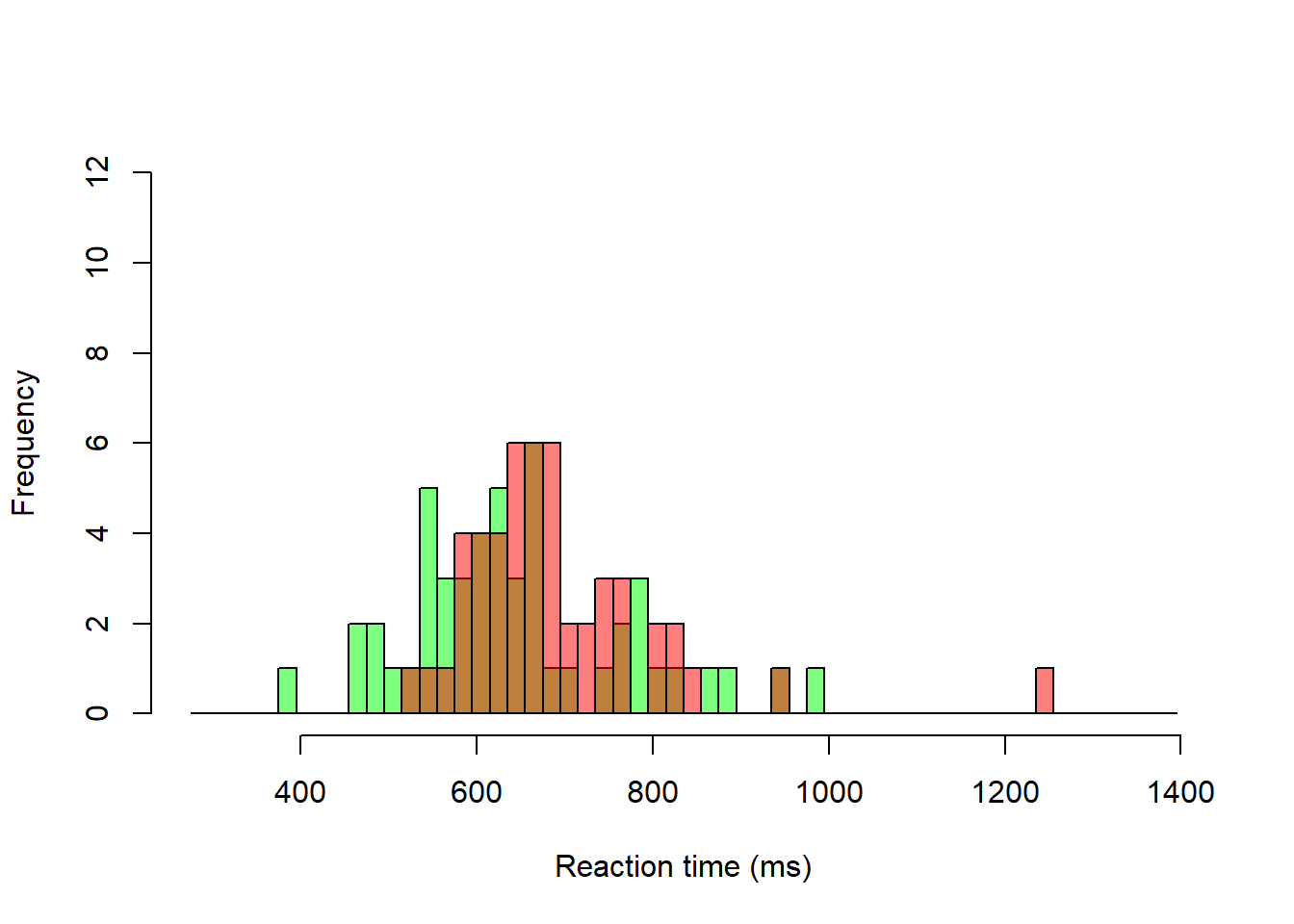

Density overlays for “Yes” and “No” trials.

# Blank histogram (note argument lty = 'blank')
hist(g$rt, breaks = seq(275, max(d$rt) + 50, by = 20), freq = FALSE, lty = 'blank', 
     col = "white", main = '', xlab = "Reaction time (ms)")
# Add density for Yes trials
dens_yes <- density(g$rt[g$yesno == 1])
polygon(dens_yes, col = rgb(0, 1, 0, 0.5))

# Add density for No trials
dens_no <- density(g$rt[g$yesno == 2])
polygon(dens_no, col = rgb(1, 0, 0, 0.5))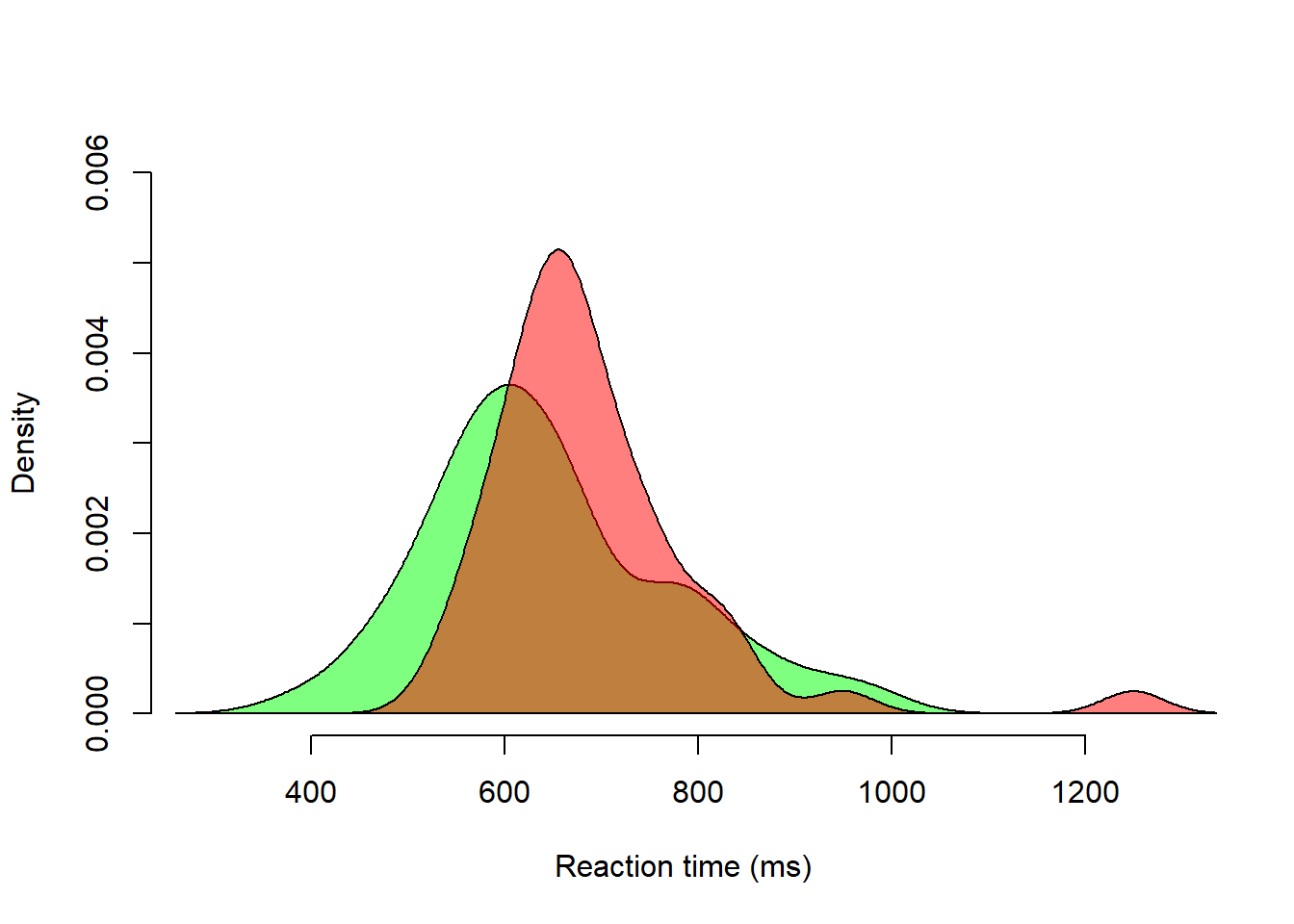

Below some descriptive statistics for the 5-item list and No-trials (red density curve above)

Boxplot

x <- g$rt[g$yesno == 2]  # Put data in vector called x, to simplify things
boxplot(x)
mtext("5-item list, No-trials", 3, line = 0.5) # Add heading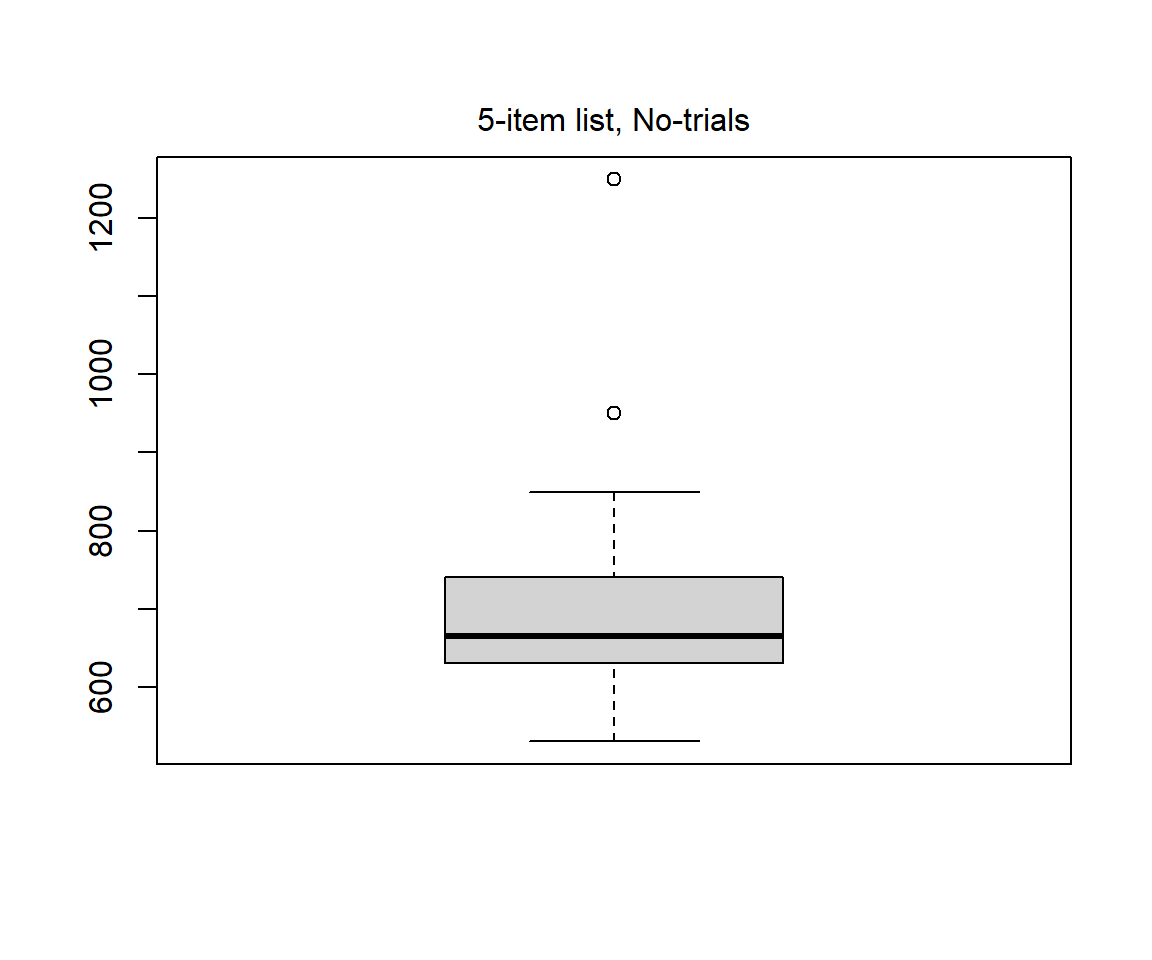

Quantiles

summary(x)  # Give five point summary, including quartiles

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  530.0   630.0   665.0   691.2   735.0  1250.0 

Central tendency (or Location)

# Mean
m <- mean(x, na.rm = TRUE)
m_rmout <- mean(x[x < 900], na.rm = TRUE) # Remove values > 900 ms

# Median
mdn <- median(x, na.rm = TRUE)
mdn_rmout <- median(x[x < 900], na.rm = TRUE) # Remove values > 900 ms

location <- c(m = m, m_rmout = m_rmout, mdn = mdn, mdn_rmout = mdn_rmout)
round(location, 1)

        m   m_rmout       mdn mdn_rmout 
    691.2     674.2     665.0     660.0 

Variation (or Dispersion or Scale)

# Standard deviation
std <- sd(x, na.rm = TRUE)
std_rmout <- sd(x[x < 900], na.rm = TRUE) # Remove values > 900 ms

# Inter-quartile range
iqr <- IQR(x, na.rm = TRUE)
iqr_rmout <- IQR(x[x < 900], na.rm = TRUE) # Remove values > 900 ms

# Median absolute deviation
# NOTE: default for mad() is with correction factor
mad <- mad(x, na.rm = TRUE)
mad_rmout <- mad(x[x < 900], na.rm = TRUE) # Remove values > 900 ms

dispersion <- c(std = std, std_rmout = std_rmout, 
                iqr = iqr, iqr_rmout = iqr_rmout,
                mad = mad, mad_rmout = mad_rmout)
round(dispersion, 1)

      std std_rmout       iqr iqr_rmout       mad mad_rmout 
    116.1      75.3     105.0      92.5      81.5      74.1 

4.3 Transformations

Linear transformations

Linear transformations changes the mean or the standard deviation or both of a set of values but will preserve the shape of the distribution of values. A kernel density plot would therefore have the same shape for a distribution of values as for a linear transformations of the same values.

Linear transformations are applied for different reasons, some examples below:

• centering. Remove the mean: \(x_{center} = x - mean(x)\). Often done before fitting a linear regression model to make the intercept meaningful or when fitting interaction models (more about this in later chapters). The mean of the centered variable will be zero, the standard deviation will remain the same.
• z-transformation. Remove the mean and set standard deviation to unity: \(z_{x} = \frac{x - mean(x)}{sd(x)}\). Can be used for the same reasons as centering, but also to set variables with different units on a common scale (unit: sd).
• transform range., e.g., set minimum = 0 and maximum = 1: \(x_{01} = \frac{x - min(x)}{max(x) - min(x)}\). This may be a way to help interpretation when x-scale has no meaningful unit, and be used to set variables with different units on a common scale (for the example above, unit: range of data).
• change unit. For example, from meters to centimeters or from USD to USDx1000 to obtain numbers that are easy to work with, or to transform from an unfamiliar to a familiar unit, for example, from degrees Fahrenheit (F) to Celsius (C): \(C = \frac{5}{9}(F - 32)\)

The figure below illustrates the preserved shape of data distributions after linear transformations of a set of (simulated) temperature measurements. But first a scatter plot matrix to verify that the variables indeed are linearly related.

set.seed(999)

# A thousand temperature measurements, all around 60 F
fahr <- rnorm(1000, mean = 60, sd = 2) 

# Transform to Celsius
celc <- (5/9) * (fahr - 32) 

# z-transform
z <-(fahr - mean(fahr))/sd(fahr)

# Scatter plot matrix, just to show that they linearly related
pairs(~ fahr + celc + z)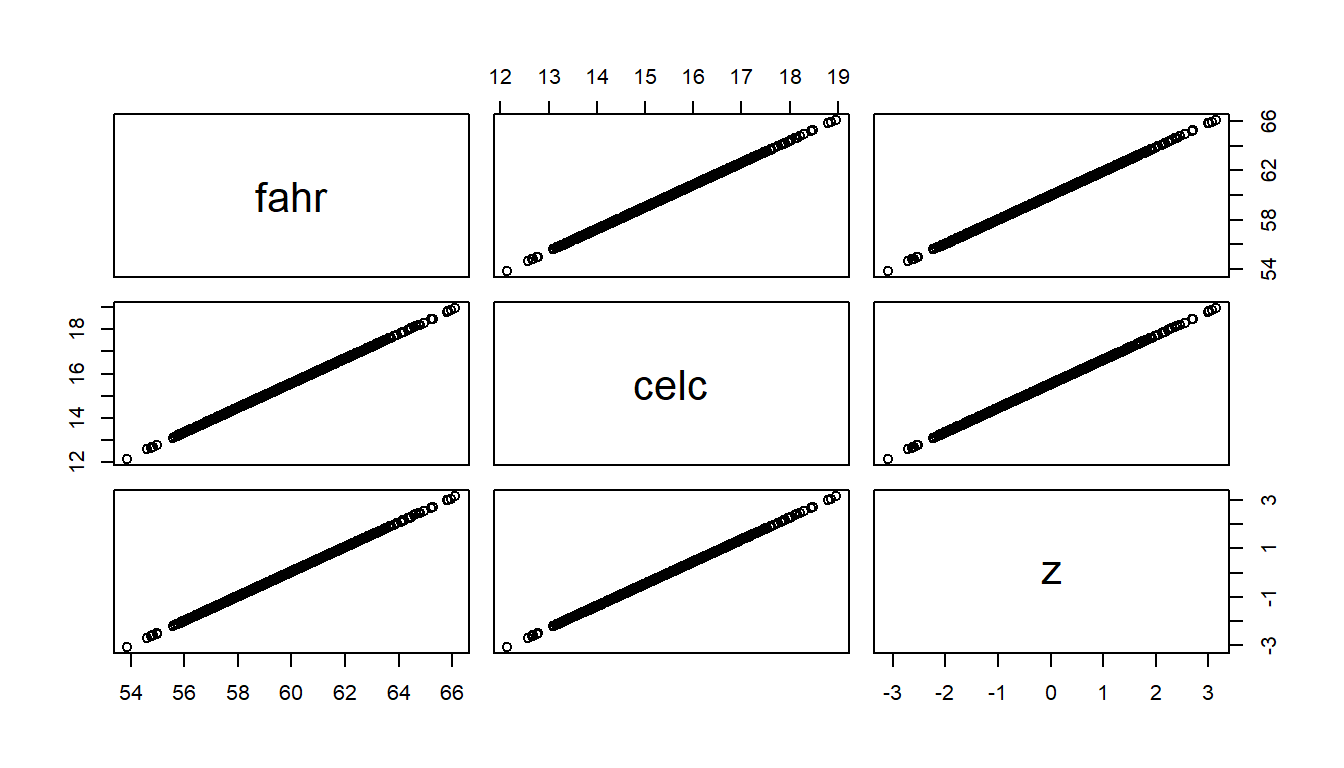

# Density plots in three panels
par(mfrow = c(1, 3))  
plot(density(fahr), main = "Fahrenheit", xlab = "Temperatur [degrees Fahrenheit]")
plot(density(celc), main = "Celcius", xlab = "Temperatur [degrees Celcius]")
plot(density(z), main = "z-score", xlab = "Temperatur [standard deviation]")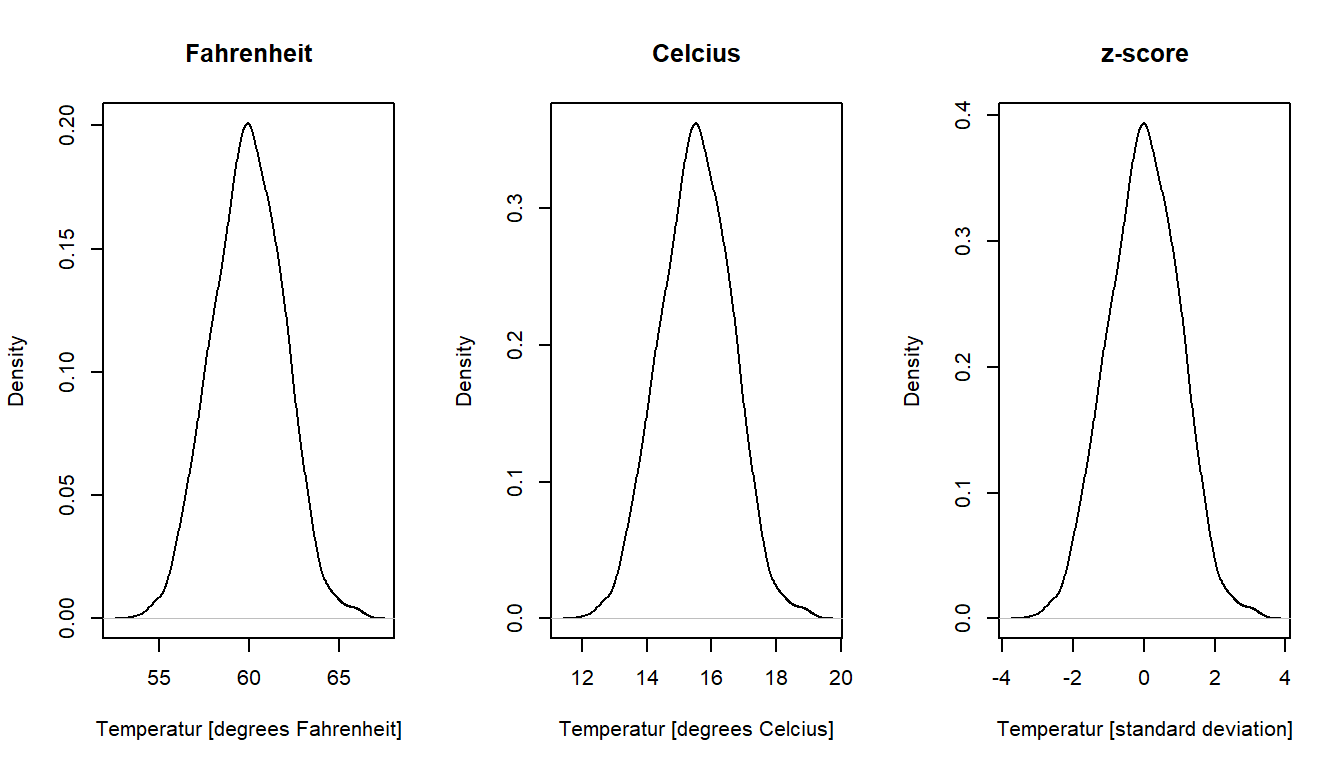

Non-linear transformations

Unlike linear transformations, non-linear transformations will change the shape of the distribution. We will talk more about reasons for non-linear transformations in regression analysis. Here I will only mention the log-transform, often used to handle skewed distributions. Reaction time is an example of a variable that typically has a positive skew, and therefore it is common to apply a log transform. Below illustrated using the reaction time data in rt_howell.txt.

Linear and log-transformed reaction times for No-trials (yesno = 2) of the five-item list (nstim = 5).

rt <- d$rt[d$yesno == 2 & d$nstim == 5]
log_rt <- log(rt)  # Natural log

par(mfrow = c(1, 2)) # Two plots

# Linear: histogram with density
hist(rt, breaks = seq(275, 1400, by = 25), 
     freq = FALSE, main = "linear")
dens_yes <- density(rt)
polygon(dens_yes, col = rgb(1, 0, 0, 0.5))

# Log: histogram with density
hist(log_rt, breaks = seq(log(275), log(1400), by = 0.05), 
     freq = FALSE, main = "natural log")
dens_yes <- density(log_rt)
polygon(dens_yes, col = rgb(1, 0, 0, 0.5))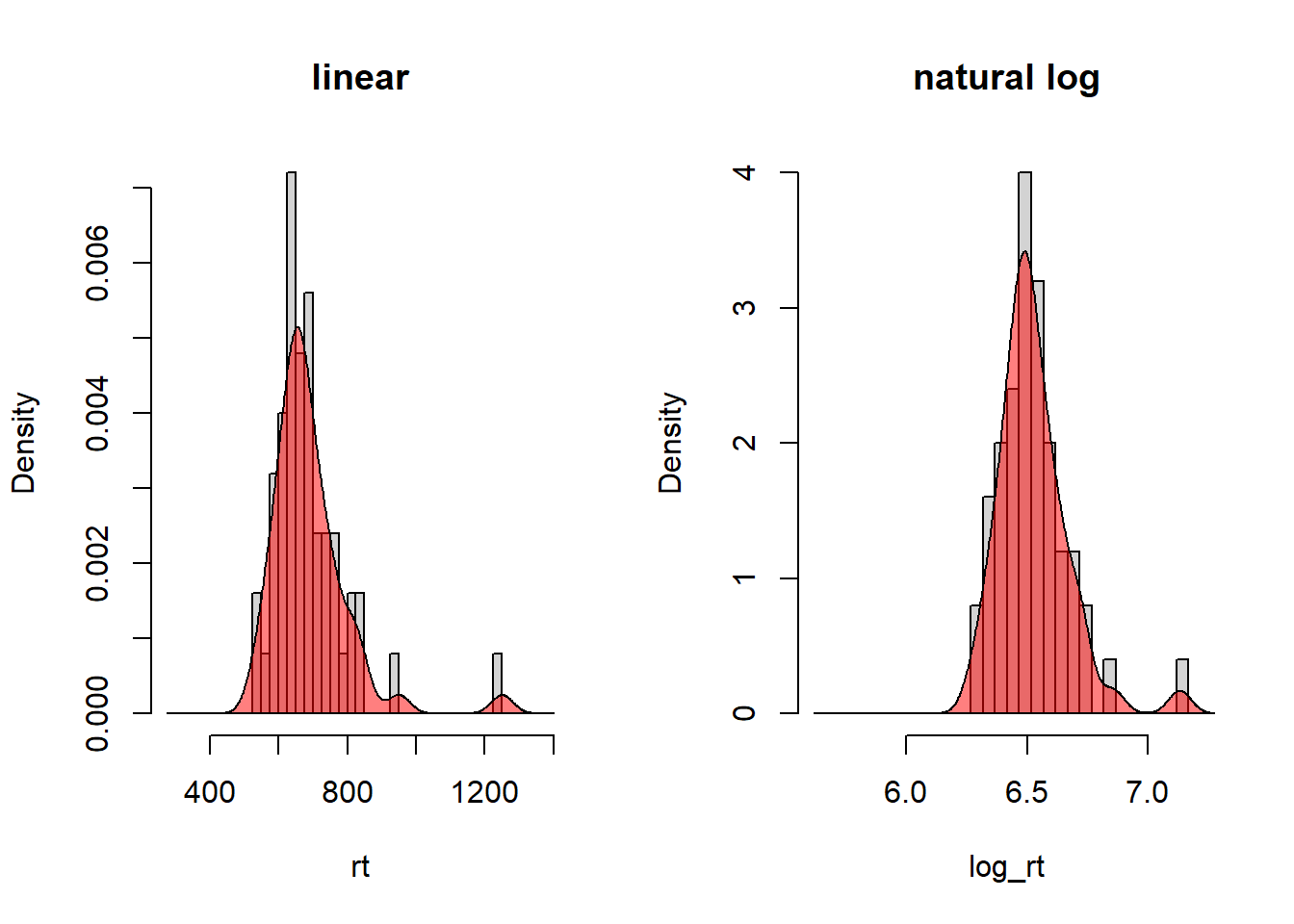

Maybe not a big difference in shape, but note that the outlier in the left panel (around 1200 ms) has moved closer to the main bulk of the data in the right panel.

The base of the log doesn’t matter for the shape of the distribution, it will remain the same. This because log-transformed values of different bases are linearly related, for example, \(log_{10}(x) = \frac{log_e(x)}{log_e(10)}\), and as we saw above, linear transformations doesn’t change the shape of a distribution.

4.4 Probability 2: Probability distributions

Gelman et al. (2021) define “probability distribution” in an informal way that also defines “random variable”:

A probability distribution corresponds to an urn with a potentially infinite number of balls inside. When a ball is drawn at random, the “random variable” is what is written on this ball.

Gelman et al. (2021), Section 3.5, p. 40

For discrete variables, there is a finite set of balls (outcomes) in proportion to their probability (so twice as many balls for an outcome twice as probable as another outcome). For continuous variables, the set is infinite, because there are infinitely many numbers in any interval of a continuous variable. Still, there will be more balls with numbers in a given interval than in another.

We will focus on the Normal distribution in this course, but let’s start with the Binomial distribution.

Binomial Distribution

The Binomial distribution may be thought of as the “coin-tossing” distribution: It gives you the probability of the number of outcomes classified as “successes” (e.g., “heads”) in \(n\) independent trials with two outcomes (e.g., a coin toss), each with success probability \(p\) (\(p = 0.5\) for a fair coin, \(p \neq 0.5\) for an unfair coin).

Notation

The notation \(Y \sim Binomial(n, p)\) means that the random variable \(Y\) is distributed as the Binomial distribution with \(n\) independent trials, each with probability \(p\) of success. Y can take on the values 0, 1, …, n. 

A special case of this distribution occurs when \(n = 1\), known as the Bernoulli distribution. The notation \(Y \sim Bernoulli(p)\) means that \(Y\) is distributed as the Binomial distribution with \(n = 1\), where \(Y\) can take on only the values 0 or 1.

\(P(Y = y) = \binom{n}{y}p^y(1-p)^{n-y}\) gives the probability of \(y\) successes in \(n\) trials, where \(\binom{n}{y}\) is the number of ways you can draw \(y\) objects from a set of \(n\) objects, if order doesn’t matter (try out the choose() function in R).

Expected value (mean value): \(E(Y) = np\)

Standard deviation: \(SD(Y) = \sqrt{np(1-p)}\)

Example: Calculate the probability of two successes in three trials, if \(p = 0.6\)

\(Y \sim Binomial(n = 3, p = 0.6)\)

\(P(Y = 2) = \binom{3}{2}p^2(1-p)^{1} = 3 * 0.6 * 0.6 * 0.4 = 0.432\)

Calculate by hand in R

# Using equation
p <- 0.6
yprob <- choose(3,2) * p^2 * (1-p)^1
yprob 

[1] 0.432

# Using R's binomial function
dbinom(x = 2, size = 3, p = 0.6)

[1] 0.432

Probability mass function (PMF)

A Probability mass function gives the probability for each outcome of a discrete random variable. It sums to one.

Example: Plot PMF for n = 19, and p = 0.2, 0.5, 0.8

n <- 19
p <- c(0.2, 0.5, 0.8)

# Panels next to each other
par(mfrow = c(1, 3))

# Plots
binpmf <- function(n = 19, p) {
  y <- 0:n  # Possible outcomes
  m1 <- dbinom(y, size = n, prob = p)
  plot(y, m1, type = 'h', xlab = "y",
     ylab  = "P(Y = y)", ylim = c(0, 0.3), lwd = 3)
  mtext(sprintf("n = %d, p = %0.1f", n, p), 3, cex = 1)
  lines(c(-1, n+1), c(0, 0), col = "grey")
}

binpmf(p = p[1])
binpmf(p = p[2])
binpmf(p = p[3])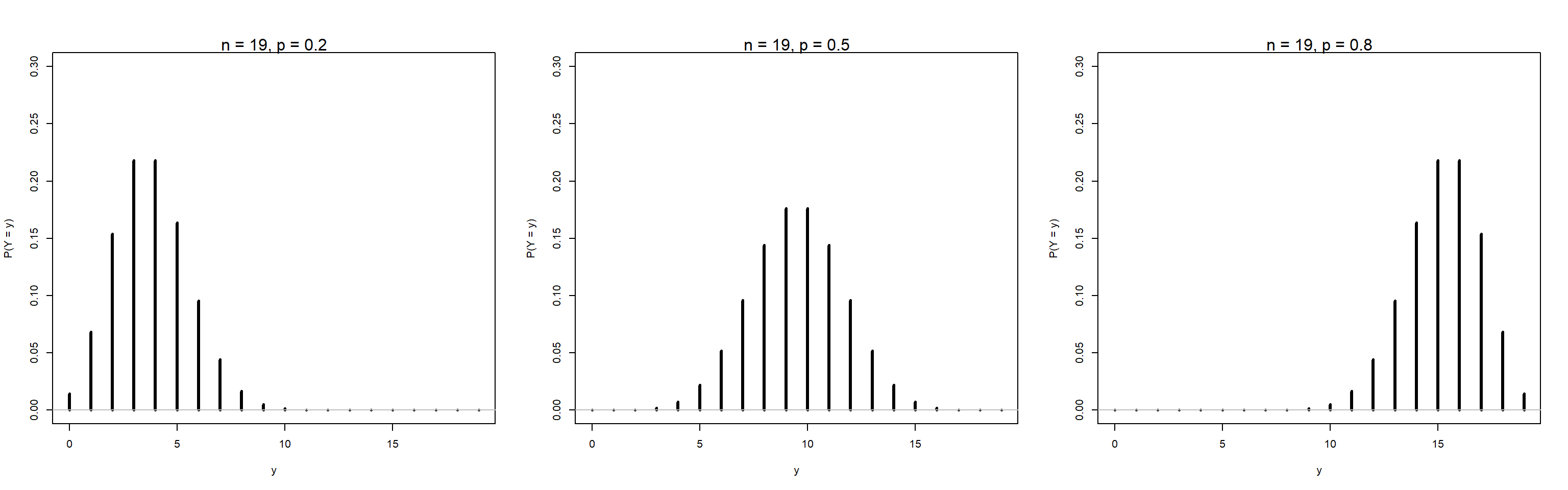

Cumulative distribution function (CDF)

The cumulative distribution function (CDF) gives the probability that a random variable is less than or equal to a specific value.

Example: Plot CDF for n = 19, and p = 0.2, 0.5, 0.8

n <- 19
p <- c(0.2, 0.5, 0.8)

# Panels next to each other
par(mfrow = c(1, 3))

# Plots
bincdf <- function(n = 19, p) {
  y <- 0:n  # Possible outcomes
  m1 <- pbinom(y, size = n, prob = p)
  plot(y, m1, type = 's', xlab = "y",
     ylab  = "P(Y <= y)", ylim = c(0, 1), lwd = 1.5)
  mtext(sprintf("n = %d, p = %0.1f", n, p), 3, cex = 0.8)
  lines(c(-1, n+1), c(0, 0), col = "grey")
}

bincdf(p = p[1])
bincdf(p = p[2])
bincdf(p = p[3])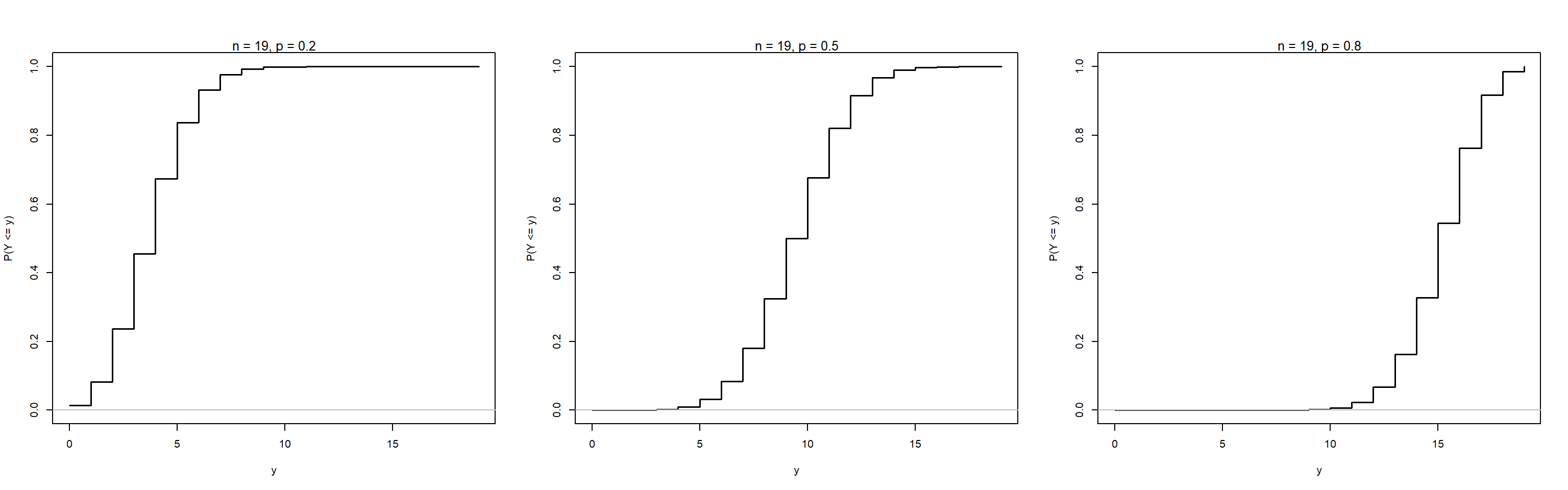

The Binomial distribution becomes approximately normal as \(n\) gets very large. Here illustrated for \(p\) = 0.2 and \(n\) = 6, 60, and 600.

n <- c(6, 60, 600)
p <- 0.2

# Panels next to each other
par(mfrow = c(1, 3))

# Plots
binpmf2 <- function(n, p, nmin, nmax) {
  y <- nmin:nmax  # Possible outcomes
  m1 <- dbinom(y, size = n, prob = p)
  plot(y, m1, type = 'h', xlab = "y",
     ylab  = "P(Y = y)", ylim = c(0, max(m1)), lwd = 1)
  mtext(sprintf("n = %d, p = %0.1f", n, p), 3, cex = 0.8)
  lines(c(-1, n+1), c(0, 0), col = "grey")
}

binpmf2(n = n[1], p = p, nmin = 0, nmax = 6)
binpmf2(n = n[2], p = p, nmin = 0, nmax = 30)
binpmf2(n = n[3], p = p, nmin = 85, nmax = 155)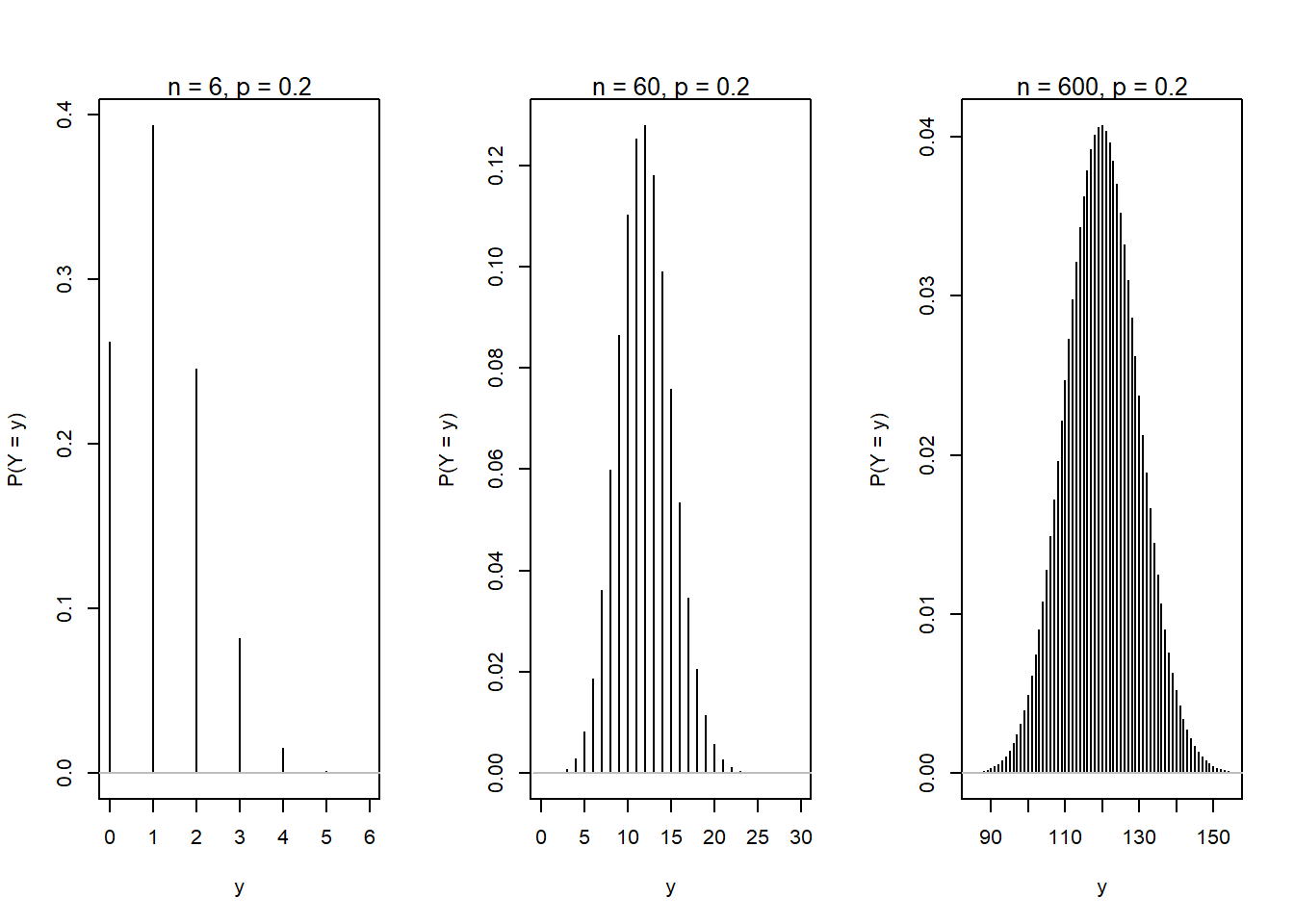

Normal Distribution

The sum of many small independent random variables will be approximately distributed as the Normal distribution (this follows from the Central Limit Theorem).

Notation

\(Y \sim N(\mu, \sigma)\), random variable Y is distributed as a normal distribution with location (mean) \(\mu\) and scale (sd) \(\sigma\) (Note, the second parameter is often given as the variance \(\sigma^2\).)

Example: Y is scores on an IQ-test, normally distributed with mean = 100, sd = 15: \(Y \sim N(\mu=100, \sigma=15)\)

Probability density function (PDF)

For a discrete variable, the probability mass function (PMF) sums to one (see examples above). For a continuous variable, the probability density function (PDF) has an area under the curve equal to one.

iq <- seq(from = 50, to = 150, by = 1)
iqdens <- dnorm(iq, mean = 100, sd = 15)
plot(iq, iqdens, type = 'l', xlab = "y [IQ-score]", ylab = "density")
    lines(c(40, 160), c(0, 0), col = "grey")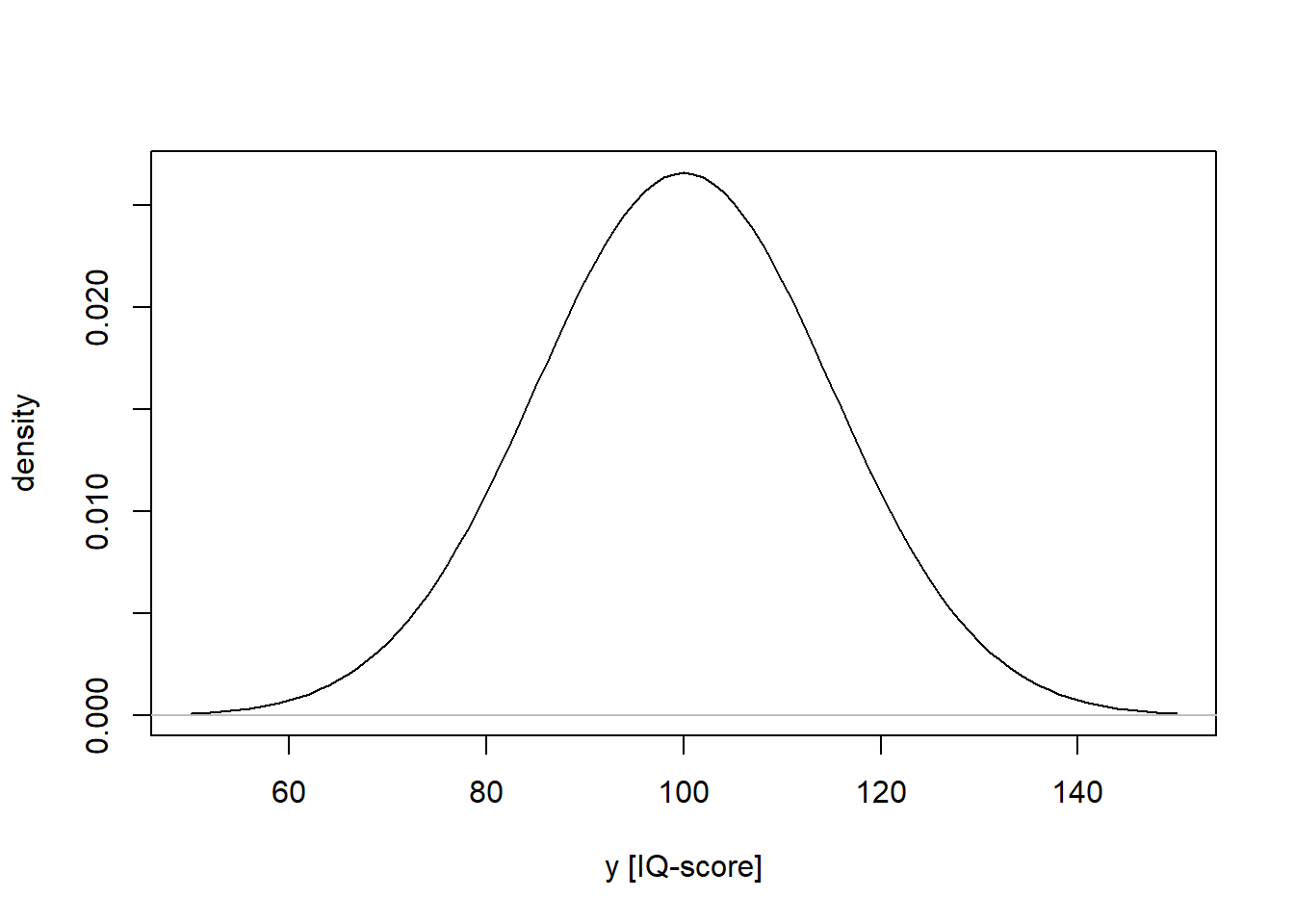

NOTE: Density is not the same as probability. It can be greater than 1!

# Denisty for uniform(0, 0,5)
x <- seq(from = -0.1, to = 0.6, by = 0.0001)
xdens <- dunif(x, min = 0, max = 0.5)
plot(x, xdens, type = 'l', xlab = "x", ylab = "density", ylim = c(0, 2.2))
lines(c(-0.2, 0.7), c(0, 0), col = "grey")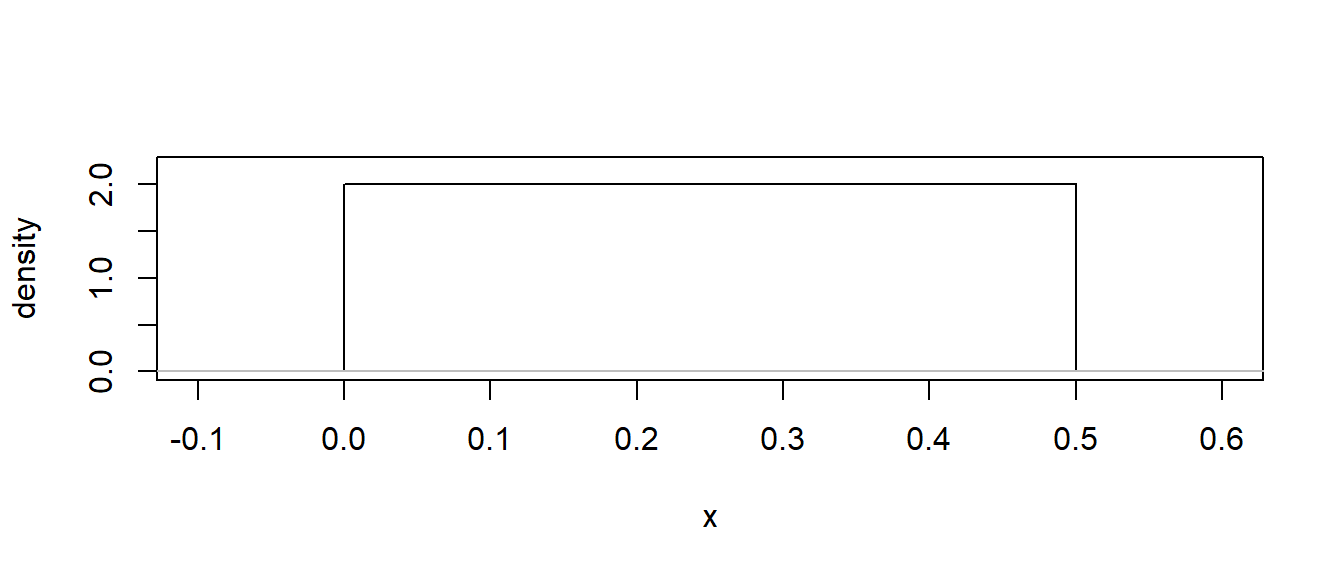

What is the probability that a randomly selected individual has an IQ-score of exactly 100, if \(IQ \sim N(\mu=100, \sigma=15)\)? The probability correspond to an area under the curve (PDF) of the normal distribution. The answer to the question depends on what we mean with “exactly”. If we really mean it, as in \(100.000000...\), then the answer is \(P(IQ = 100.000...) = 0\), because the area under the curve has zero width. But I guess that IQ-scores are measured without decimals, if so, \(IQ = 100\) can be interpreted as \(99.5 < IQ < 100.5\). This is an interval, and an area under the curve can be calculated: \(P \approx .03\).

par(mfrow = c(1, 2))

# Draw PDF, and add line for mu = 100.0000...
iq <- seq(from = 50, to = 150, by = 1)
iqdens <- dnorm(iq, mean = 100, sd = 15)
plot(iq, iqdens, type = 'l', xlab = "y [IQ-score]", ylab = "density",
     xlim = c(70, 130))
lines(c(40, 160), c(0, 0), col = "black")
lines(c(100, 100), c(0, dnorm(100, mean = 100, sd = 15)), 
      col = "grey", lwd = 0.2, lty = 3)

# Draw PDF, and add area for 99.5 < mu < 100.5
iq <- seq(from = 50, to = 150, by = 1)
iqdens <- dnorm(iq, mean = 100, sd = 15)
plot(iq, iqdens, type = 'l', xlab = "y [IQ-score]", ylab = "density",
     xlim = c(70, 130))
lines(c(40, 160), c(0, 0), col = "black")
mm <- seq(99.5, 100.5, 0.01)
d <- dnorm(mm, mean = 100, sd = 15)
polygon(x = c(mm, rev(mm)), y = c(rep(0, length(d)), rev(d)),
          col = rgb(0, 0, 0, 0.1), border = FALSE)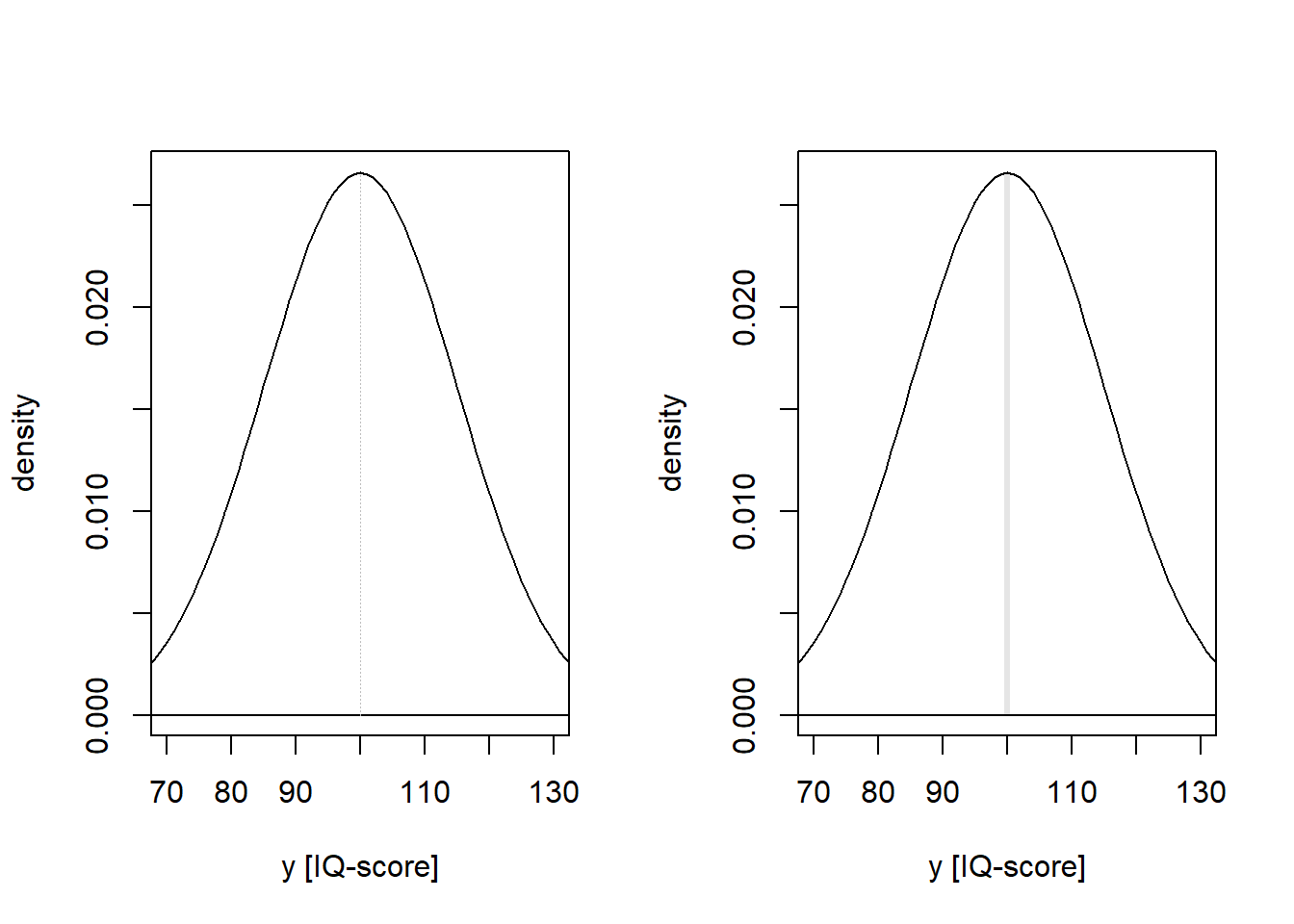

Calculate probability (area under the curve):

# P(mu == 100)  
pnorm(100, mean = 100, sd = 15) -  pnorm(100, mean = 100, sd = 15)

[1] 0

# P(mu > 99.5 | mu < 100.5)
pnorm(100.5, mean = 100, sd = 15) -  pnorm(99.5, mean = 100, sd = 15)

[1] 0.02659123

Cumulative distribution function (CDF)

The CDF has the same definition for discrete and continuous variables: It gives the probability that a random variable is less than or equal to a specific value of a random variable.

iq <- seq(from = 50, to = 150, by = 1)
iqcdf <- pnorm(iq, mean = 100, sd = 15)
plot(iq, iqcdf, type = 'l', xlab = "y [IQ-score]", ylab = "P(Y < y)")
lines(c(40, 160), c(0, 0), col = "grey")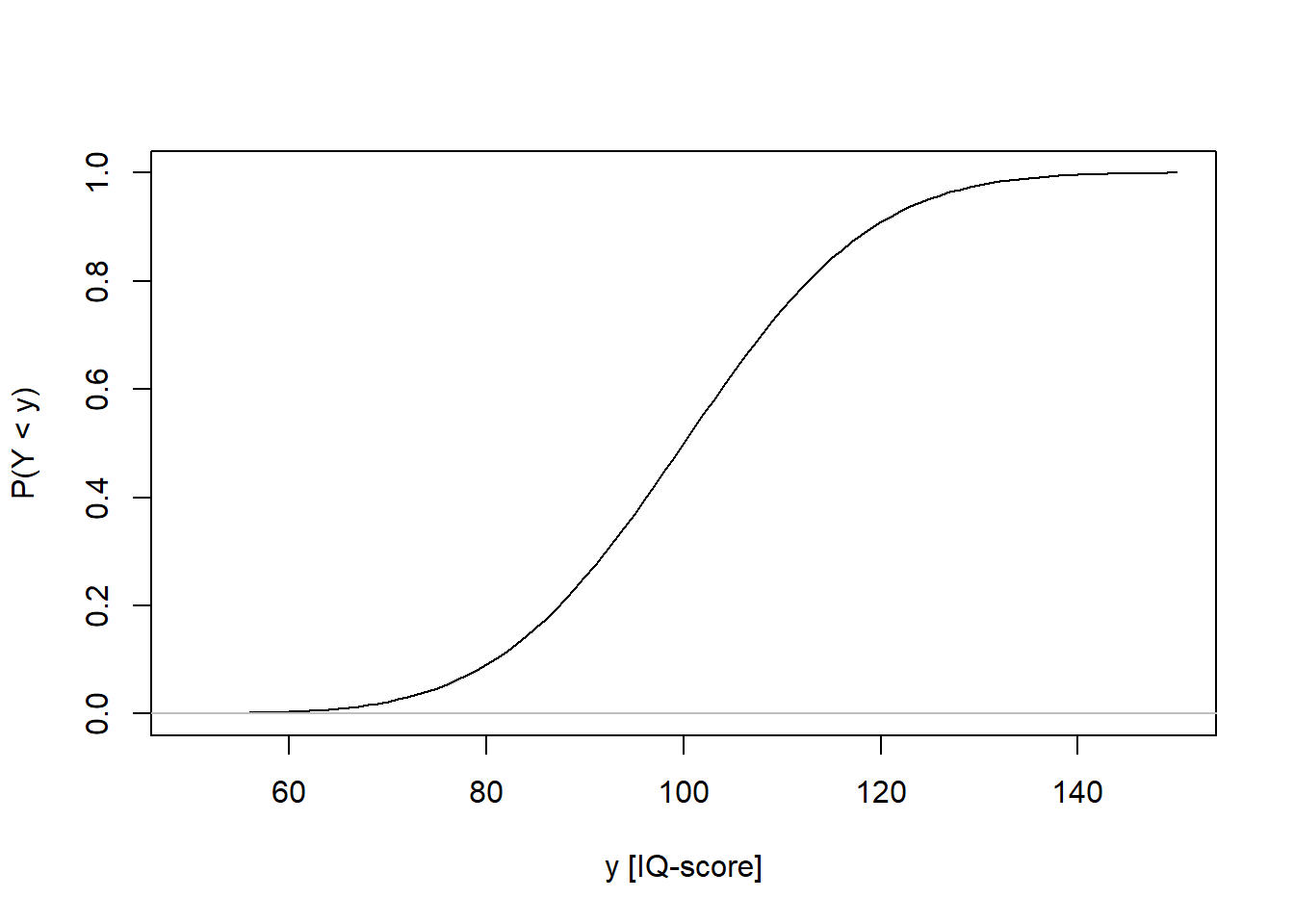

Location and scale of normal distribution

This plot shows three normal distributions with…

• Left panel: Same location (mean), different scale (standard deviation)

• Right panel: Different location, same scale

x <- seq(from = 0, to = 100, by = 1)

par(mfrow = c(1, 2))

# Different scales, same location 
plot(x, dnorm(x, 50, 10), ylim = c(0, 0.2), pch = "", xlab = "x", ylab = "density")
lines(x, dnorm(x, 50, 2), col = "red")
lines(x, dnorm(x, 50, 10))
lines(x, dnorm(x, 50, 20), col = "blue")

# Different location, same scale 
plot(x, dnorm(x, 50, 10), ylim = c(0, 0.2), pch = "", xlab = "x", ylab = "density")
lines(x, dnorm(x, 30, 3), col = "red")
lines(x, dnorm(x, 50, 3))
lines(x, dnorm(x, 55, 3), col = "blue")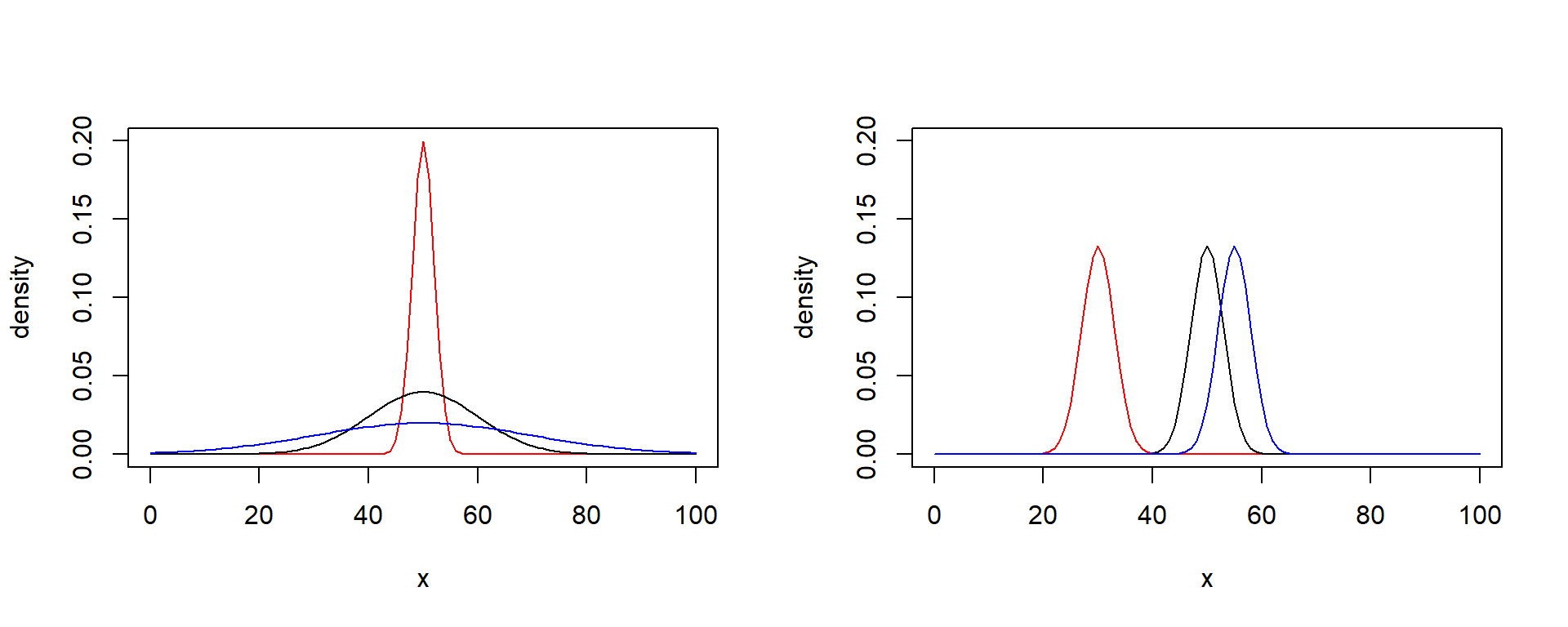

Standard normal

Remember that linear transformations doesn’t change the shape of distributions. The standard normal is just a linear transformation (z-scores) of another normal distribution with the purpose of setting \(\mu = 0\) and \(\sigma = 1\).

\(Y \sim N(\mu, \sigma)\) Original (non-standard) normal,

\(Z = (Y - \mu)/\sigma\) Linear transformation,

\(Z \sim N(0, 1)\) Standard normal.

par(mfrow = c(1, 2))
z <- seq(-4, 4, 0.1)

# PDF
dd <- dnorm(z)
plot(z, dd, type = 'l', ylab = "density")
lines(c(-5, 5), c(0, 0), col = "grey")
mtext("PDF", 3, cex = 0.8)

# CDF
dd <- pnorm(z)
plot(z, dd, type = 'l', ylab = "probability, P(Z <= z)")
lines(c(-5, 5), c(0, 0), col = "grey")
mtext("CDF", 3, cex = 0.8)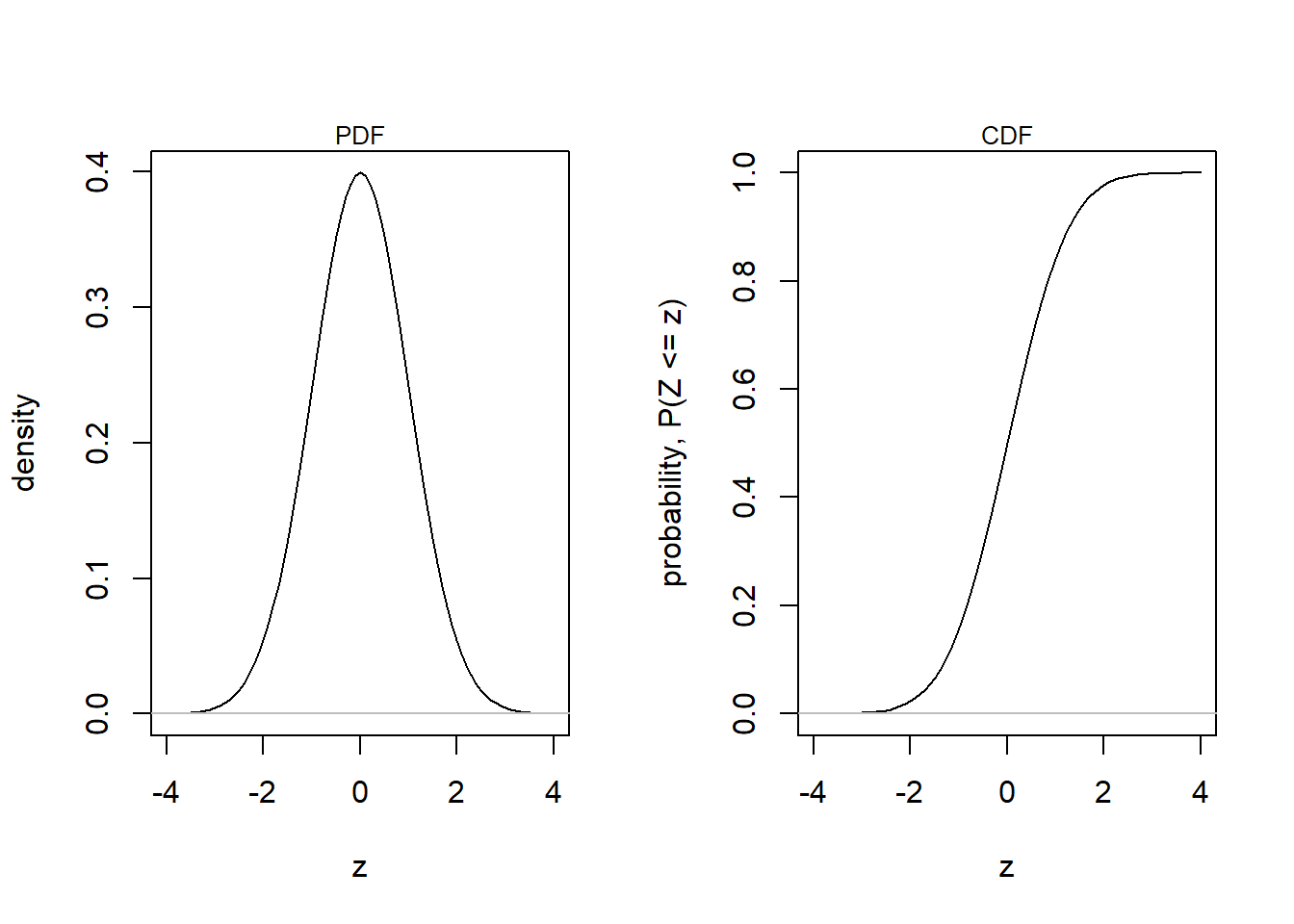

The 68-95-99.7 rule

The 68-95-99.7 rule, also known as the empirical rule, describes the distribution of data in a normal distribution. According to this rule:

• Approximately 68 % of the data falls within one standard deviation of the mean. Put equivalently, the probability that a random observation, \(x\) falls within one standard deviation of the mean is approximately 0.68, that is, \(Pr(\mu - \sigma < x < \mu + \sigma) \approx 0.68)\)

• About 95 % of the data lies within two standard deviations of the mean.

• About 99.7 % of the data is found within three standard deviations of the mean.

For the standard normal, \(N(\mu = 0, \sigma = 1)\), these three intervals corresponds to the intervals [-1, 1], [-2, 2], and, [-3, 3], respectively.

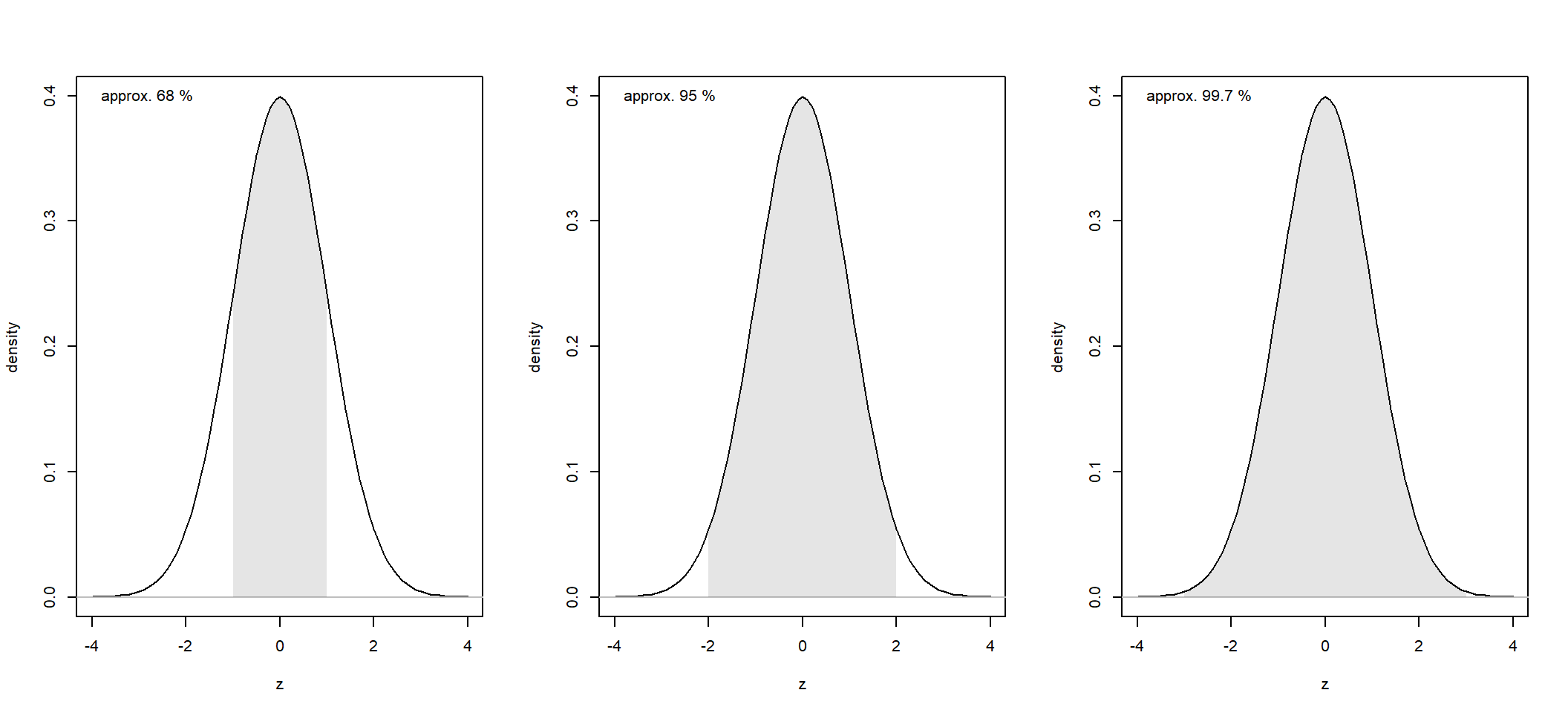
In R, you can calculate the exact probabilities like this:

# Calculate (pm1sd for +/- 1 sd, etc.)
pm1sd <- pnorm(1) - pnorm(-1)
pm2sd <- pnorm(2) - pnorm(-2)
pm3sd <- pnorm(3) - pnorm(-3)

# Round and print
round(c(pm1sd = pm1sd, pm2sd = pm2sd, pm3sd = pm3sd), 5)

  pm1sd   pm2sd   pm3sd 
0.68269 0.95450 0.99730 

How normal is the Normal?

Example from Gelman et al. (2021), Fig. 3.6:

Assume that height is normally distributed, with different means for men and women:

• Men: \(h_{male} \sim N(\mu = 180, \sigma = 8)\), unit cm.
• women: \(h_{female} \sim N(\mu = 168, \sigma = 8)\), unit cm.

set.seed(999)
male <- rnorm(5e4, 180, 8)
female <- rnorm(5e4, 168, 8)
combined <- c(male, female)

# Blank histogram (note argument lty = 'blank')
hist(male, breaks = seq(120, 230, by = 20), freq = FALSE, lty = 'blank',
     col = "white", main = '', xlab = "Height (cm) ", ylim = c(0, 0.06))
# Add density for Yes trials
dens_male <- density(male)
polygon(dens_male, col = rgb(0, 1, 0, 0.5))

# Add density for No trials
dens_female <- density(female)
polygon(dens_female, col = rgb(1, 0, 0, 0.5))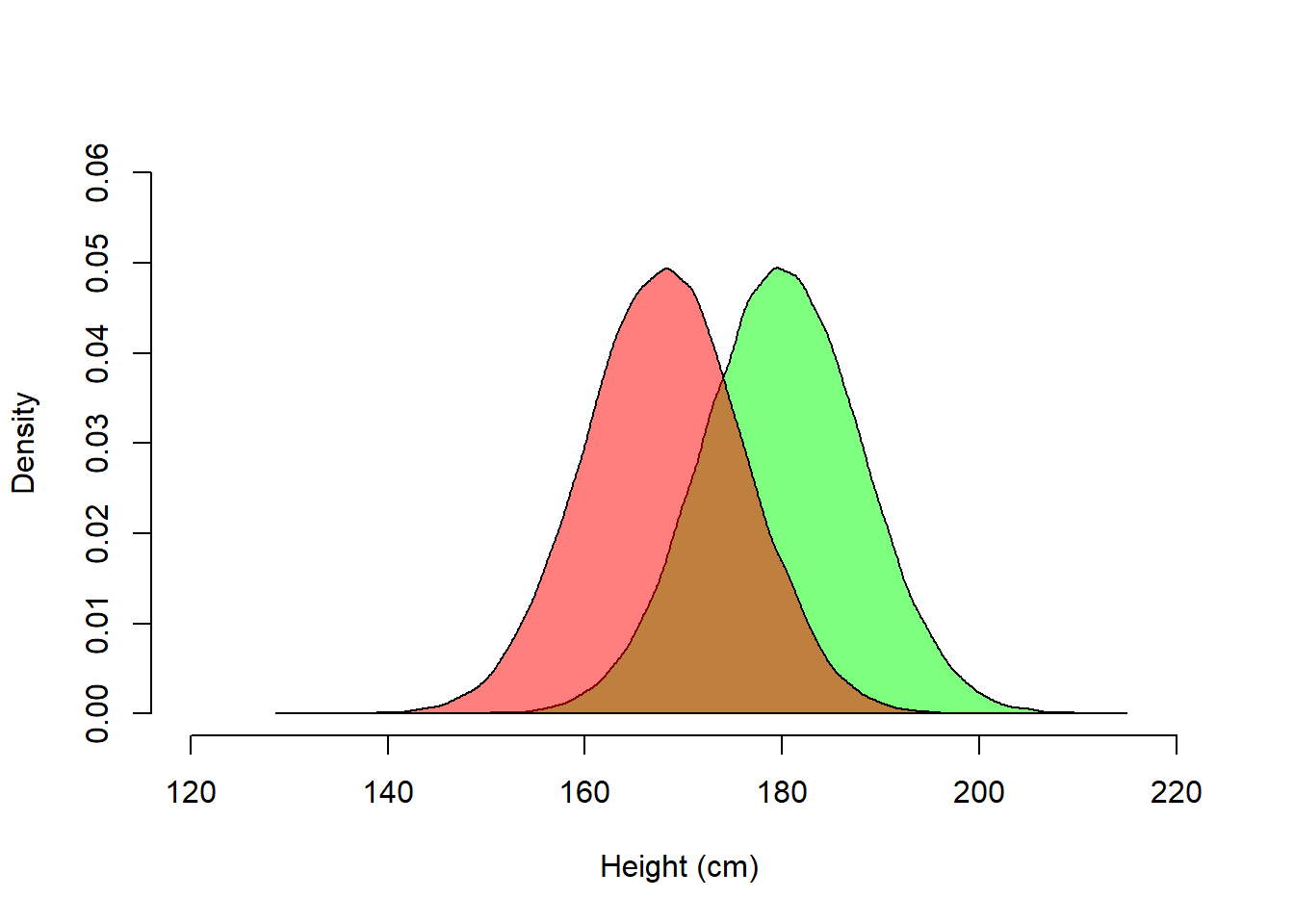

Height in the combined population of men and women is however not normally distributed.

# Blank histogram (note argument lty = 'blank')
hist(combined, breaks = seq(120, 230, by = 20), freq = FALSE, lty = 'blank', 
     col = "white", main = '', xlab = "Height (cm) ", ylim = c(0, 0.06))
# Add density for Yes trials
dens_combined <- density(combined)
polygon(dens_combined, col = rgb(0, 0, 1, 0.5))

The density plot for the combined population looks normal, but actually it is not. If normally distributed, about 84 % of values are less than 1 standard deviation above the mean. This is true for our simulated male and female populations, but not for the combined population.

# Exact probability of x < 1, if X ~ N(mean = 0, sd = 1)
pnorm(1)  

[1] 0.8413447

# Estimate from our simulated male population
mean(male < mean(male) + sd(male))

[1] 0.8416

# Estimate from our female popualtion
mean(female < mean(female) + sd(female)) 

[1] 0.84062

# Estimate from the combined popualtion
mean(combined < mean(combined) + sd(combined))

[1] 0.83395

A common method for evaluating normality is to visualize using so called QQ-plots (points fall on the red line if the data is perfectly normal). QQ-plots are not part of the course, but I use them here to drive home the point that the (simulated) combined population (vector combined) is not normally distributed.

# QQ-plot
zmale <- (male - mean(male))/sd(male)
zfemale <- (female - mean(female))/sd(female)
zcombined <- (combined - mean(combined))/sd(combined)
ylim <- c(-4, 4)
par(mfrow = c(1, 3))
qqnorm(zmale, main = "Population male weight, z-score", cex = 0.7, ylim = ylim)
qqline(zmale, col = "red")
qqnorm(zfemale, main = "Population female weight, z-score", cex = 0.7, ylim = ylim)
qqline(zfemale, col = "red")
qqnorm(zcombined, main = "Population combined, z-score ", cex = 0.7, ylim = ylim)
qqline(zcombined, col = "red")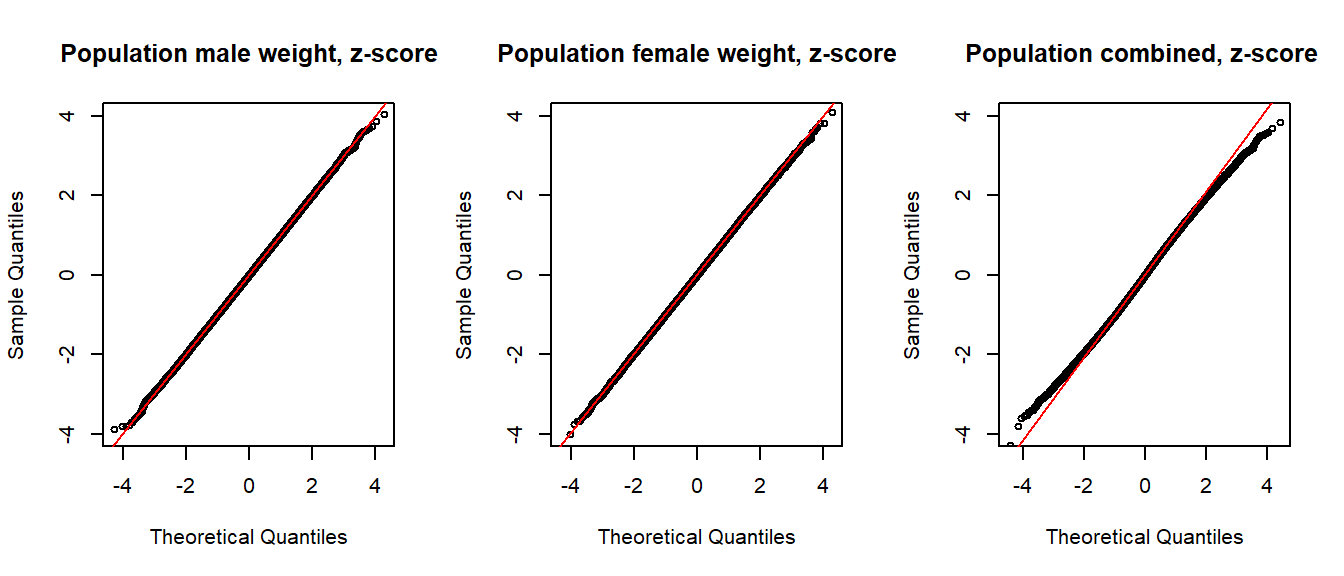

Practice

Practice problems are labeled Easy (E), Medium (M), and Hard (H), (as in McElreath (2020)).

Easy

4E0. Identify two advantages and two disadvantages of using the arithmetic mean compared to the median as sample statistics for measuring central tendency.

4E1. The median absolute deviation (MAD) is often multiplied by a constant, why and what is the constant?

Note: In the regression outputs from rstanarm::stan_glm(), they call MAD multiplied by this constant for MAD_SD.

4E2. Below a frequency table of number of children (0, 1, 2, 3, or 4) in a sample 200 families.

Calculate by hand the following statistics for number of children in these families:

1. Median
2. Maximum
3. Inter-quartile range
4. Median absolute deviation (Hint. It is the same with or without normalizing constant)

set.seed(123)
n_child <- sample(0:4, size = 200, replace = TRUE, prob = c(5, 10, 1, 1, 0))
n_child_f <- factor(n_child, levels = 0:4)
table(Children = n_child_f)

Children
  0   1   2   3   4 
 54 119  16  11   0 

4E3. Below is a boxplot.

Approximate the following by eye:

1. Inter-quartile range (IQR).
2. Median (IQR).
3. Range
4. Whether distribution is symmetric, positively or negatively skewed

set.seed(123)
y <- rlnorm(60, log(10), log(2.5))
boxplot(y, xlab = "X", horizontal = TRUE)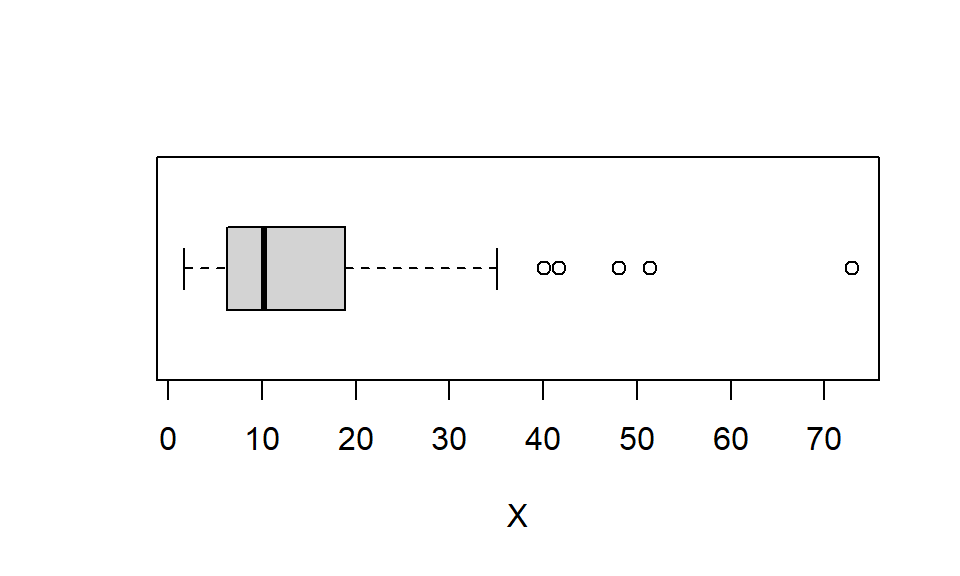

# round(c(iqr = IQR(y)), 0)

4E4. This dataset is from an experiment with 80 participants, evenly split into two groups of 40 participants: A control group (group = 0) and an experimental group (group = 1). The results are visualized using boxplots.

Approximate by eye (and brain!):

1. Difference in median scores between groups
2. Approximately how many in the experimental group that performed better than the median of the control group
3. Variability of scores: Was it similar in the two groups?

set.seed(123)
n <- 40
group <- c(rep(0, n), rep(1, n))
y <- rnorm(length(group), (10 + 2*group), (3 - 1*group))

# plot
boxplot(y ~ group, xlab = "Group", ylab = "Outcome", horizontal = FALSE)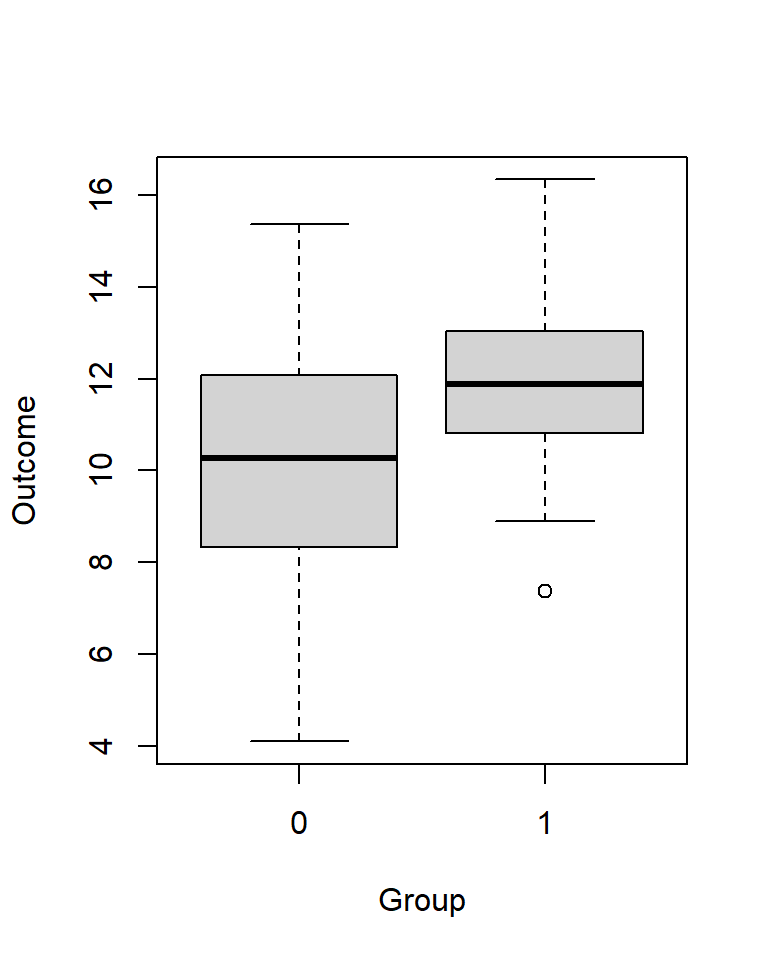

4E5. Below is a kernel density plot of a dataset with an arithmetic mean of 26. Which of the following values is closest to the median: 7, 10, 21, 27, 41?

set.seed(123)
y <- 10 * rlnorm(100, mean = log(2), sd = log(2))
plot(density(y), xlab = "X", main = "")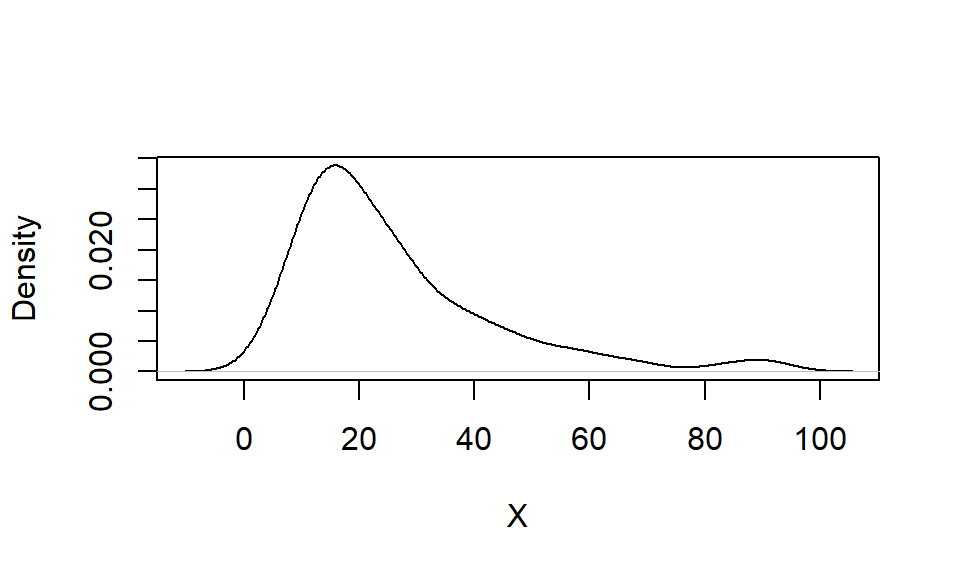

# median(y)

4E6. One advantage of a kernel density plot over a histogram is that its shape is not influenced by the choice of bin size. Explain.

4E7. Simulate a sample of reaction times [ms] using this code:

set.seed(123)
rt <- rlnorm(1e3, meanlog = 6, sdlog = 0.69)

Calculate:

1. Mean
2. Median
3. Standard deviation
4. Inter-quartile range
5. Median absolute deviation

4E8. Visualize the distribution of data from 4E7 (vector rt) using a histogram overlaid with a kernel density plot (see examples above). Locate the bins of the histogram at multiples of \(50 \pm 25 \ \ ms\).

4E9. Repeat 4E8 but now with log reaction time log(rt). Make as many bins as in 4E8.

Note: In hist(), the argument breaks = k creates k equally spaced bins.

4E10.

1. Make two boxplots, one for rt and the other for log(rt), using data from 4E7.
2. How many observations were classified as outliers according to the boxplot rule for rt and for log(rt).

4E11. Assume that the waist circumference among Swedish middle aged men (40-60 y) is normally distributed with mean = 100 cm and standard deviation = 7 cm.

Calculate the probability that a randomly selected man form this population has a waist circumference …

1. above 94 cm,
2. within \(100 \pm 10\) cm,
3. either below 85 cm or above 115 cm,
4. within the middle 50 % of the distribution.

Hint: A useful function in R is pnorm().

4E12. Below a standard normal distribution. For each panel, approximate by eye (and brain!) the probability that a random observation would fall in the shaded region. Use the 68-95-99.7 rule where appropriate.

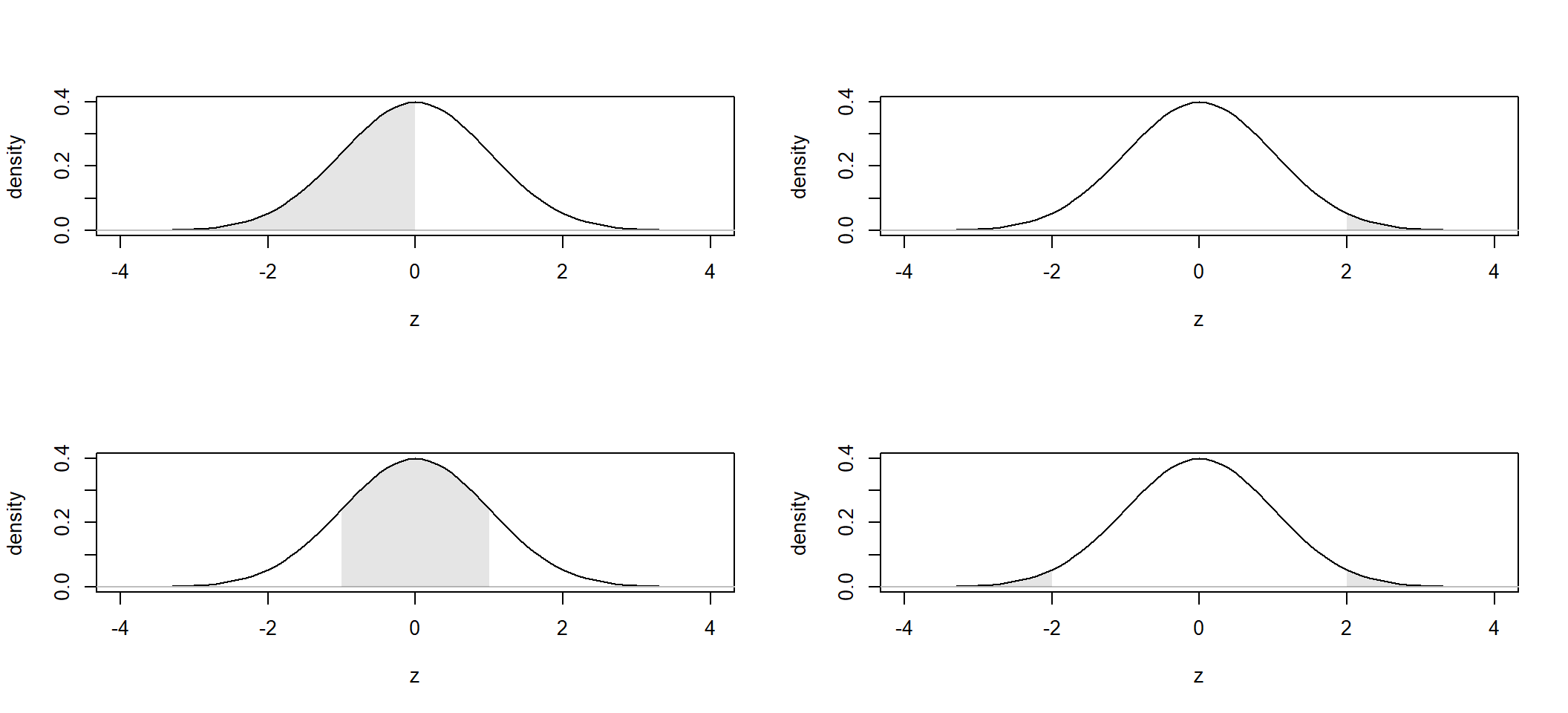
4E13. Use R to calculate exact answer (to 5 decimals) for the probabilities in 4E12.

Hint: A useful function in R is pnorm().

Medium

4M1.

1. Search the internet for “geometric mean” and then explain in your own words what it is and when to use it.
2. Calculate the geometric mean of the sample in 4E7 (vector rt). Here is one way to do it in R: exp(mean(log(rt))).
3. Was the geometric mean for the sample close to the population geometric mean? To find the latter, decipher the simulation code in 4E7.

4M2. Student X is taking an exam with 10 multiple choice questions, each with 5 response alternatives of which one is the correct answer. X has no clue and responds randomly.

1. Illustrate the Probability Mass Function (PMF), that is, make a diagram with the probabilities of each of the possible outcomes 0, 1, …, 10 correct answers (see examples above, the function dbinom() is helpful)
2. Calculate the probability that he answers correct on exactly 4 questions
3. Calculate the probability that he answers correct on 4 or more questions

4M3. Below is a kernel density plot of a data set.

1. Based on the plot, suggest an interval within which you are 50 % confident that the arithmetic mean value of the dataset lies. That is, you would feel equally surprised whether your interval includes the mean or not.
2. Suggest an interval within which you are 95 % confident that the mean value of the dataset lies. So you would be much more surprised if your interval does not include the mean than if it does.

I realize it’s a somewhat unusual question, but think of it as an exercise in thinking about subjective probability.

set.seed(321)
y1 <- -10 * rlnorm(1000, mean = log(5), sd = log(1.5)) + 199
y2 <- rnorm(100, mean = 100, sd = 10)
y <- c(y1, y2)
plot(density(y), xlab = "X", ylab = "", main = "", axes = FALSE)
axis(1, at = seq(40, 200, 5), cex.axis = 0.8)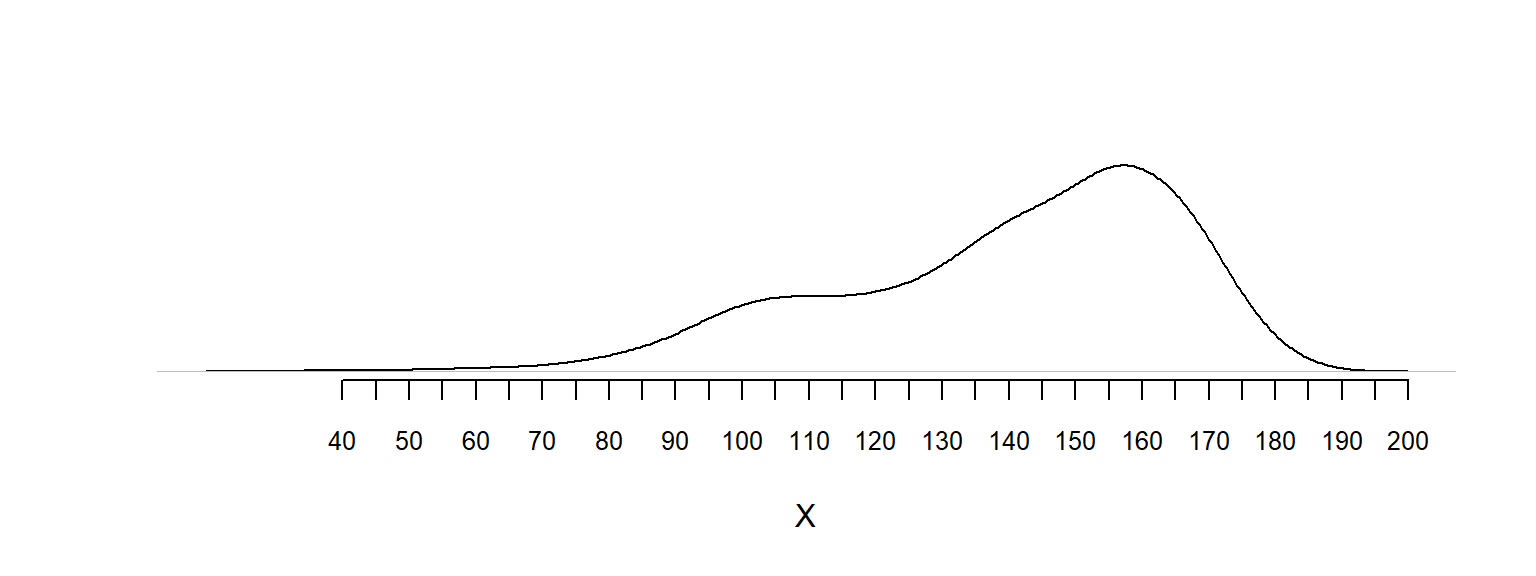

# median(y)
# mean(y)

4M4. This is a data set of 7 observations: \(y = [1, 3, 3, 4, 4, 5, 8]\), with
\(mean(y) = 4\).

1. Calculate the minimum and maximum values after mean-centering this dataset.
2. Apply the transformation ynew = (y - mean(y))/(0.1*sd(y)). What is the mean and standard deviation of ynew.
3. Transform the data to have a minimum = 0 and maximum = 70. What is the median value of this transformed data.

4M5. Create a data set with 7 observations that has mean = 100 and sd = 15 (exactly). Describe your method by providing R-code.

Hard

4H1. Go back to 4E11 and answer this question: What is the probability that a randomly selected man has a waist-circumference of 96 cm? Answer in a way that also explains the difference between probability and density.

4H2.

1. Draw the distribution from which the reaction time data in 4E7 was simulated. (You may look at the R-code that I used to draw normal distributions in the notes above).
2. Calculate the probability that a randomly drawn observation from the distribution would be greater than 1000 ms.
3. Calculate the probability that a randomly drawn observation would be between 200 and 800 ms.

4H3. Simulation is fun! And useful! 4E11(d) was maybe too easy (answer = 0.5). A harder version would ask for the waist-circumference interval corresponding to the middle 50 % of the data. My answer is \([95.3, 104.7]\) (rounded to 1 decimal). Use simulation to verify (or falsify) my answer.

4H4. Use pnorm() and qnorm() to calculate the exact interval in 4H3. Report with four decimals.

4H5. Here another simulation exercise:

Draw 10,000 samples of size \(n = 16\) from a normal distribution with \(\mu = 100\) and \(\sigma = 15\). For each sample, calculate a t-value, that is, calculate

\(t = \frac{\mu - \bar{x}}{s_{x}/\sqrt(n)}\),

where \(\bar{x}\) is the sample mean and \(s_{x}\) is the sample standard deviation.

1. Plot the distribution of your 10,000 t-values in a histogram overlaid with a kernel density plot.
2. Figure out a way to demonstrate that the distribution is not normal (although it looks pretty normal).
3. In fact (as you know), your sample means follows a T-distribution with df = n-1. Use the function dt() in R to draw this distribution on your histogram from (a).

(Session Info)

sessionInfo()

R version 4.4.2 (2024-10-31 ucrt)
Platform: x86_64-w64-mingw32/x64
Running under: Windows 11 x64 (build 26100)

Matrix products: default


locale:
[1] LC_COLLATE=Swedish_Sweden.utf8  LC_CTYPE=Swedish_Sweden.utf8   
[3] LC_MONETARY=Swedish_Sweden.utf8 LC_NUMERIC=C                   
[5] LC_TIME=Swedish_Sweden.utf8    

time zone: Europe/Stockholm
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] MASS_7.3-61

loaded via a namespace (and not attached):
 [1] htmlwidgets_1.6.4 compiler_4.4.2    fastmap_1.2.0     cli_3.6.5        
 [5] tools_4.4.2       htmltools_0.5.8.1 rstudioapi_0.17.1 yaml_2.3.10      
 [9] rmarkdown_2.29    knitr_1.50        jsonlite_2.0.0    xfun_0.52        
[13] digest_0.6.37     rlang_1.1.6       evaluate_1.0.3   

Gelman, A., Hill, J., & Vehtari, A. (2021). Regression and other stories. Cambridge University Press.

Howell, D. C. (2012). Statistical methods for psychology. Cengage Learning.

McElreath, R. (2020). Statistical rethinking: A bayesian course with examples in r and stan. Chapman; Hall/CRC.