12  S: Linear Regression: Multiple Predictors

Load R-libraries

# Load the library "rstanarm" to fit Bayesian linear models using the function 
# stan_glm() 
library(rstanarm)

Topics

• Linear transformations. Discussed earlier, here some new examples
• Multiple regression
  • Combining indicator and continuous predictors, see example with weight and age.
  • Add quadratic term to model non-linear trend
  • Several continuous predictors.
• Regression diagnostics
• Assumptions behind multiple regression

Readings:

• Gelman et al. (2021), Chapter 10 on multiple predictors, Chapter 11 on assumptions and regression diagnostics, Chapter 12 on linear transformations (Sections 12.1 - 12.3).

12.1 Multiple regression

Bivariate regression involves a single predictor. Adding more than one predictor to the model makes it a multiple regression model. Multiple predictors may be included for at least two reasons:

• Prediction. Several predictors may improve the model’s ability to predict future observations
• Casual inference. If we are estimating the causal effect of an exposure variable on the outcome variable, adding additional predictors (“covariates”, i.e., potential confounders) may justify a causal interpretation of the regression coefficient for the exposure variable.

Data: sat_howell.txt

Here an example of a simple multiple regression model with surprising reversal of trend compared to simple bivariate model. Data from Table 15.1 in Howell’s “Statistical Methods for Psychology” (8th ed).

The data is based on a paper by Guber (1999) regarding the relationship between state spendings on education and students performance on two standardized tests (SAT and ACT), data is from 1994-95. Data is from the 50 U.S. states (so unit of observation is state). SAT scores range from 200 to 800, the ACT range between 1 and 36. SAT has been characterized as mainly a test of ability, whereas the ACT is more of a test of material covered in school.

Code book:

• id – id number of state
• State – Name of state
• Expend – Average annual expenditures per student (unit: 1000 USD)
• PTratio – Pupil/teacher ratio (average in state)
• Salary – Average annual salary for teachers (unit: 1000 USD)
• PctSAT – Percentage of students in the state that takes the SAT test
• Verbal – Average SAT score on the verbal part of tests
• Math – Average SAT score on the math part of tests
• SAT – Average combined SAT score
• PctACT – Percentage of students in the state that takes the ACT test
• ACT – Average combined ACT score

Follow this link to find data Save (Ctrl+S on a PC) to download as text file

h <- read.table("./datasets/sat_howell.txt", header = TRUE, sep = ',')

Research question: Estimate the causal effect of State school spendings (expend) on SAT-scores (sat)

Analyses below uses the following variables:

• SAT (sat): Outcome variable. This is the mean performance on ability test
• Expend (expend): Independent variable. How much the state spends on education
• logPctSAT (psat) as covariate. This is the log of the percentage of students in the state taking the SAT. Reasons for taking the log: often done with proportions, makes it less truncated.
• State (state) Name of State
• Salary (salary) Average teacher salary
• PTratio (ptratio) Average pupil-to-teacher ratio

Boxplot of percentage (left) and log percentage (right) of students in the state taking the SAT.

par(mfrow = c(1, 2))
boxplot(h$PctSAT, main = "Per cent SAT takers", ylim = c(0, 100))
boxplot(log(h$PctSAT), main = "log(Per cent SAT takers)")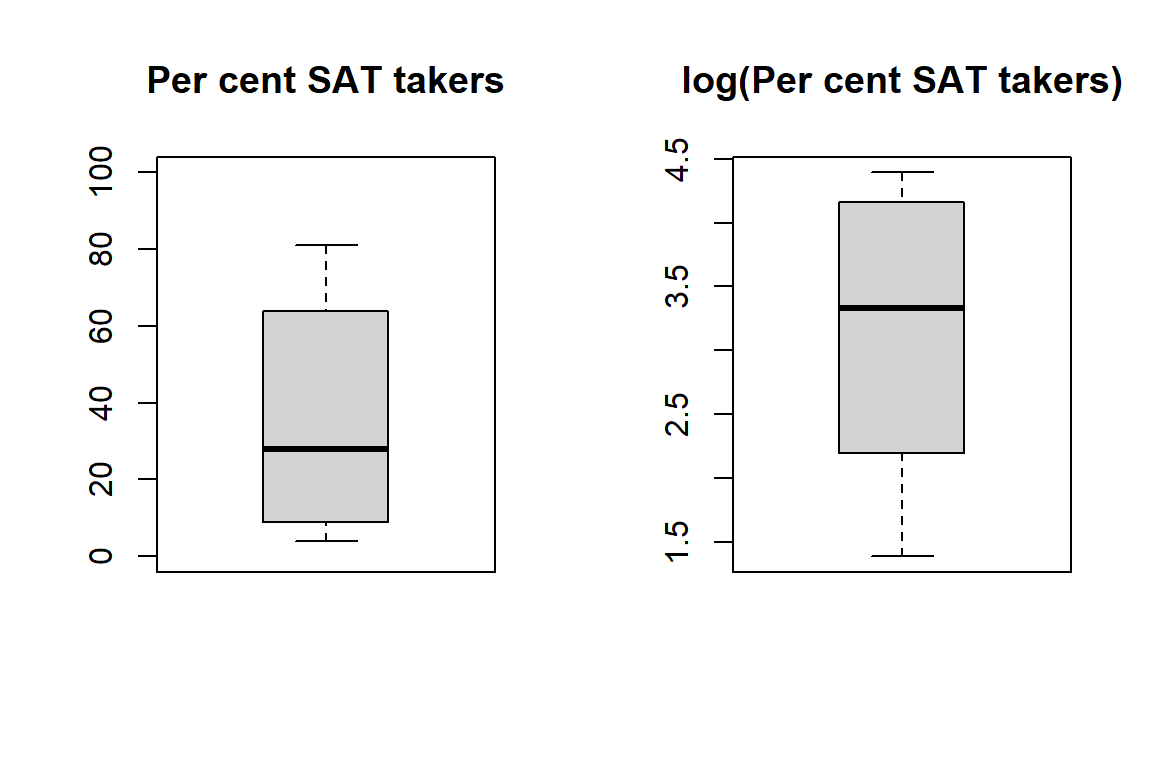

To simplify the following presentation, I put the key variables in a new data frame.

# Rename selected variables to simplify the following presentation
expend <- h$Expend
sat <- h$SAT
psat <- h$PctSAT  # log-transform, log() in R is the natural log ln
psatlog <- log(h$PctSAT)  # log-transform, log() in R is the natural log ln
state <- h$State
ptratio <- h$PTratio
salary <- h$Salary

# Put in new data frame called d
d <- data.frame(state, expend, psat, psatlog, ptratio, salary, sat)
str(d)

'data.frame':   50 obs. of  7 variables:
 $ state  : chr  "Alabama" "Alaska" "Arizona" "Ark" ...
 $ expend : num  4.41 8.96 4.78 4.46 4.99 ...
 $ psat   : int  8 47 27 6 45 29 81 68 48 65 ...
 $ psatlog: num  2.08 3.85 3.3 1.79 3.81 ...
 $ ptratio: num  17.2 17.6 19.3 17.1 24 18.4 14.4 16.6 19.1 16.3 ...
 $ salary : num  31.1 48 32.2 28.9 41.1 ...
 $ sat    : int  1029 934 944 1005 902 980 908 897 889 854 ...

Take a look at the outcome variable SAT:

par(mfrow = c(1, 2))
# Histogram
hist(d$sat, breaks = seq(775, 1225, 50), freq = TRUE,
     main = "")  # Bins of 50 SAT-points

# Histogram with density overlay
hist(d$sat, breaks = seq(775, 1225, 50), freq = FALSE, main = "")  # Bins of 50 SAT-points
lines(density(d$sat))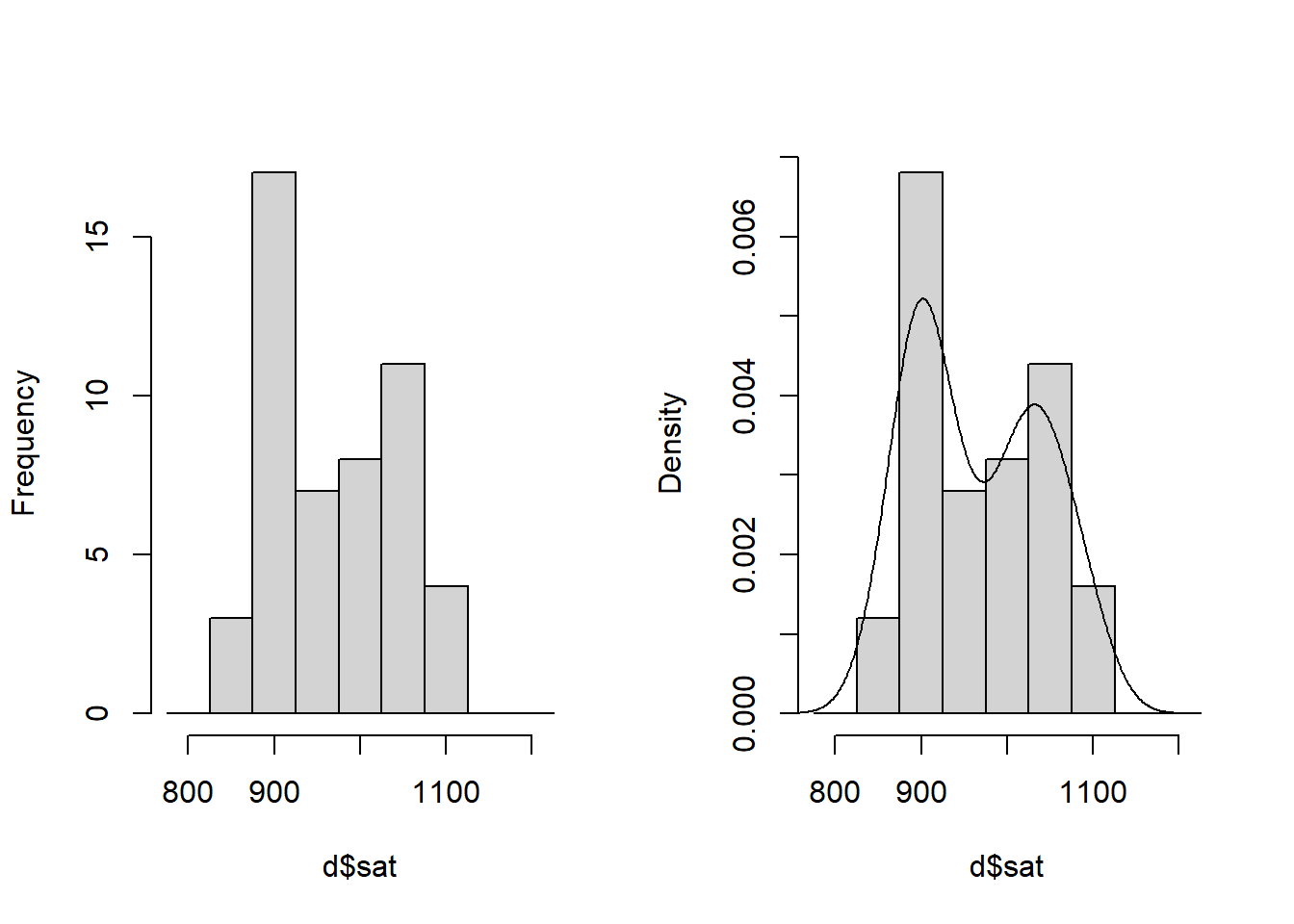

# Correlation matrix three variables of interest
round(cor(d[, 2:6]), 3)

        expend   psat psatlog ptratio salary
expend   1.000  0.593   0.561  -0.371  0.870
psat     0.593  1.000   0.961  -0.213  0.617
psatlog  0.561  0.961   1.000  -0.132  0.613
ptratio -0.371 -0.213  -0.132   1.000 -0.001
salary   0.870  0.617   0.613  -0.001  1.000

pairs(~ sat + expend + psat + psatlog, data = d)

Crude model

# Bivariate regression model
plot(d$expend, d$sat)            # Scatter plot to inspect data
crude <- glm(sat ~ expend, data = d)    # Simple (crude) regression model of SAT
summary(crude)               # Look at model output

Call:
glm(formula = sat ~ expend, data = d)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1089.294     44.390  24.539  < 2e-16 ***
expend       -20.892      7.328  -2.851  0.00641 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for gaussian family taken to be 4887.2)

    Null deviance: 274308  on 49  degrees of freedom
Residual deviance: 234586  on 48  degrees of freedom
AIC: 570.57

Number of Fisher Scoring iterations: 2

abline(crude)                # Draw regression model

# b of expend, with 95 % confidence intervals
crude_expend <- c(crude$coefficients[2], confint(crude)[2, ])
names(crude_expend) <- c('b', 'ci95lo', 'ci95hi')
round(crude_expend, 3)

      b  ci95lo  ci95hi 
-20.892 -35.255  -6.529 

Adjusted model

# Multiple regression model
adjusted = glm(sat ~ expend + psatlog, data = d) # multiple regression model
summary(adjusted)

Call:
glm(formula = sat ~ expend + psatlog, data = d)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1147.113     16.700   68.69  < 2e-16 ***
expend        11.130      3.264    3.41  0.00134 ** 
psatlog      -78.205      4.471  -17.49  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for gaussian family taken to be 664.6464)

    Null deviance: 274308  on 49  degrees of freedom
Residual deviance:  31238  on 47  degrees of freedom
AIC: 471.76

Number of Fisher Scoring iterations: 2

confint(adjusted)

                  2.5 %     97.5 %
(Intercept) 1114.380296 1179.84488
expend         4.731932   17.52733
psatlog      -86.968108  -69.44187

# 95 % confidence intervals adjusted model about b of expend
adjusted_expend <- c(adjusted$coefficients[2], confint(adjusted)[2, ])
names(adjusted_expend) <- c('b', 'ci95lo', 'ci95hi')
round(adjusted_expend, 3)

     b ci95lo ci95hi 
11.130  4.732 17.527 

Scatterplot with symbol size related to percentage SAT-takers (psat). Lines from crude model (left) and from the adjusted model (right) for states with psat at the 25th (dashed line), 50th (solid line) and the 75th (dotted line) percentile respectively.

par(mfrow = c(1, 2))
plot(d$expend, d$sat, cex = d$psatlog, pch = 21, bg = rgb(0, 1, 0, 0.1),
     xlab = "Expend", ylab = "SAT-score")
abline(crude, lty = 2)

# Lines for psat = Q25 and Q75
plot(d$expend, d$sat, cex = d$psatlog, pch = 21, bg = rgb(0, 1, 0, 0.1),
     xlab = "Expend", ylab = "SAT-score")
xlin <- c(3, 10)
ylin25 <- adjusted$coefficients[1] + 
        adjusted$coefficients[2]*xlin + 
        adjusted$coefficients[3]*quantile(d$psatlog, prob = 0.25)
lines(xlin, ylin25, col = "blue", lty = 2 )
ylin50 <- adjusted$coefficients[1] + 
        adjusted$coefficients[2]*xlin + 
        adjusted$coefficients[3]*quantile(d$psatlog, prob = 0.5)
lines(xlin, ylin50, col = "blue", lty = 1 )
ylin75 <- adjusted$coefficients[1] + 
        adjusted$coefficients[2]*xlin + 
        adjusted$coefficients[3]*quantile(d$psatlog, prob = 0.75)
lines(xlin, ylin75, col = "blue", lty = 3 )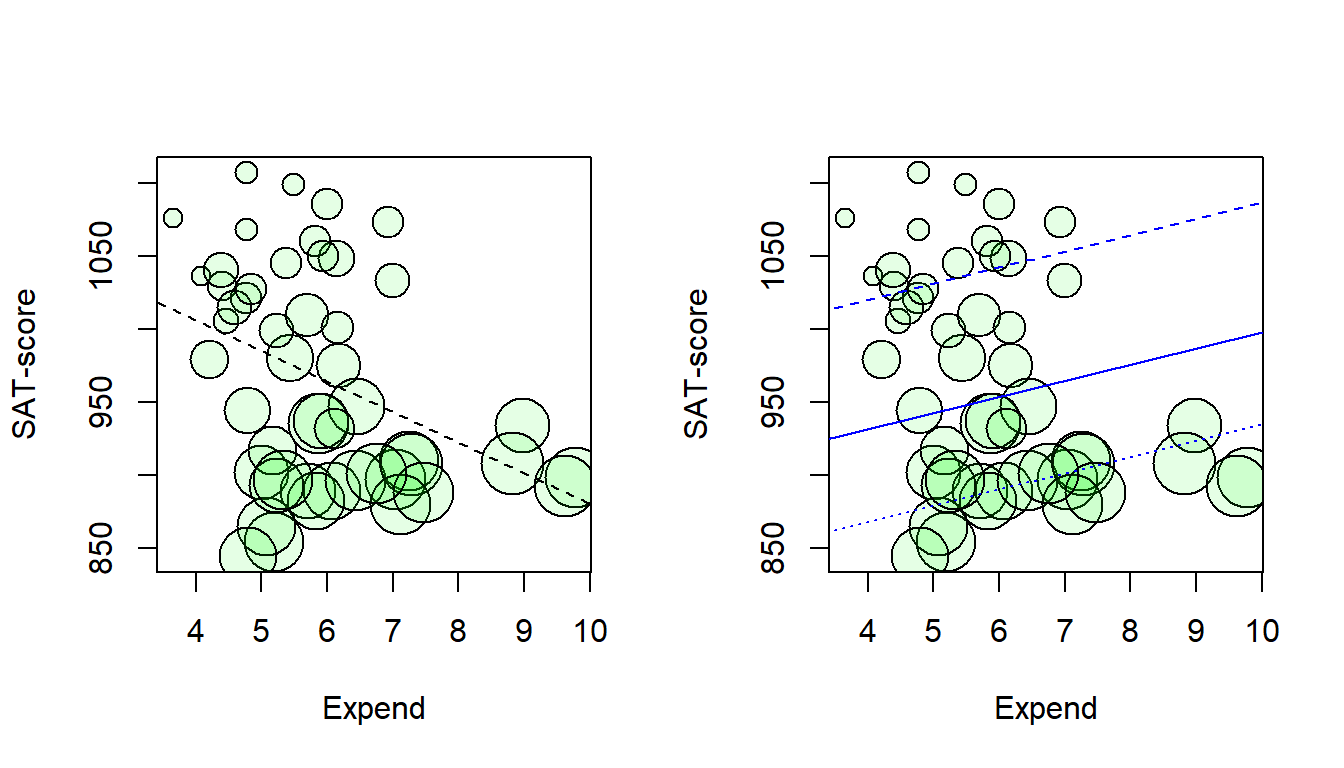

Plot effect estimates for crude and adjusted model

# create empty plot 
plot(0, xaxt = "n", xlim = c(0.5,2.5), ylim = c(-50, 50), 
     pch = "", xlab = "Model", 
     ylab = "Linear regression coefficient (SAT / Expend)")
# Add x-axis labels
axis(1, at = c(1, 2), labels = c('Crude', 'Adjusted'))


# Add dotted line (lty = 2) at no effect: regression coefficient = 0
lines(c(-0.2,3.2), c(0,0), lty = 2)

# Add CI for crude and adjusted model
arrows(x0 = 1, x1 = 1, y0 = crude_expend[2], y1 = crude_expend[3], 
       angle = 90, code = 3, length = 0.1)
points(1, crude_expend[1], pch = 21, bg = "grey")

arrows(x0 = 2, x1 = 2, y0 = adjusted_expend[2], y1 = adjusted_expend[3], 
       angle = 90, code = 3, length = 0.1)
points(2, adjusted_expend[1], pch = 21, bg = "grey")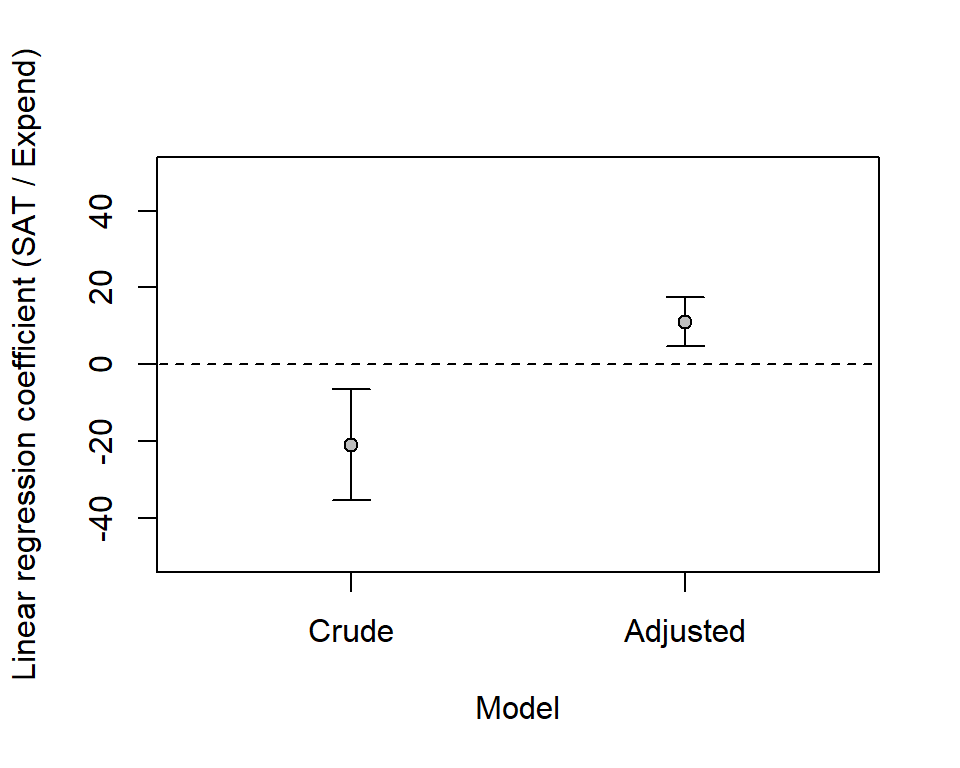

Predicted against observed data

This plot shows model predictions (adjusted model) versus observed data. Note that predictions (y-axis) refer to predicted mean values for given values of the predictors.

sat_pred <- adjusted$fitted.values
plot(sat, sat_pred, xlim = c(800, 1200), ylim = c(800, 1200))
lines(c(800, 1200), c(800, 1200))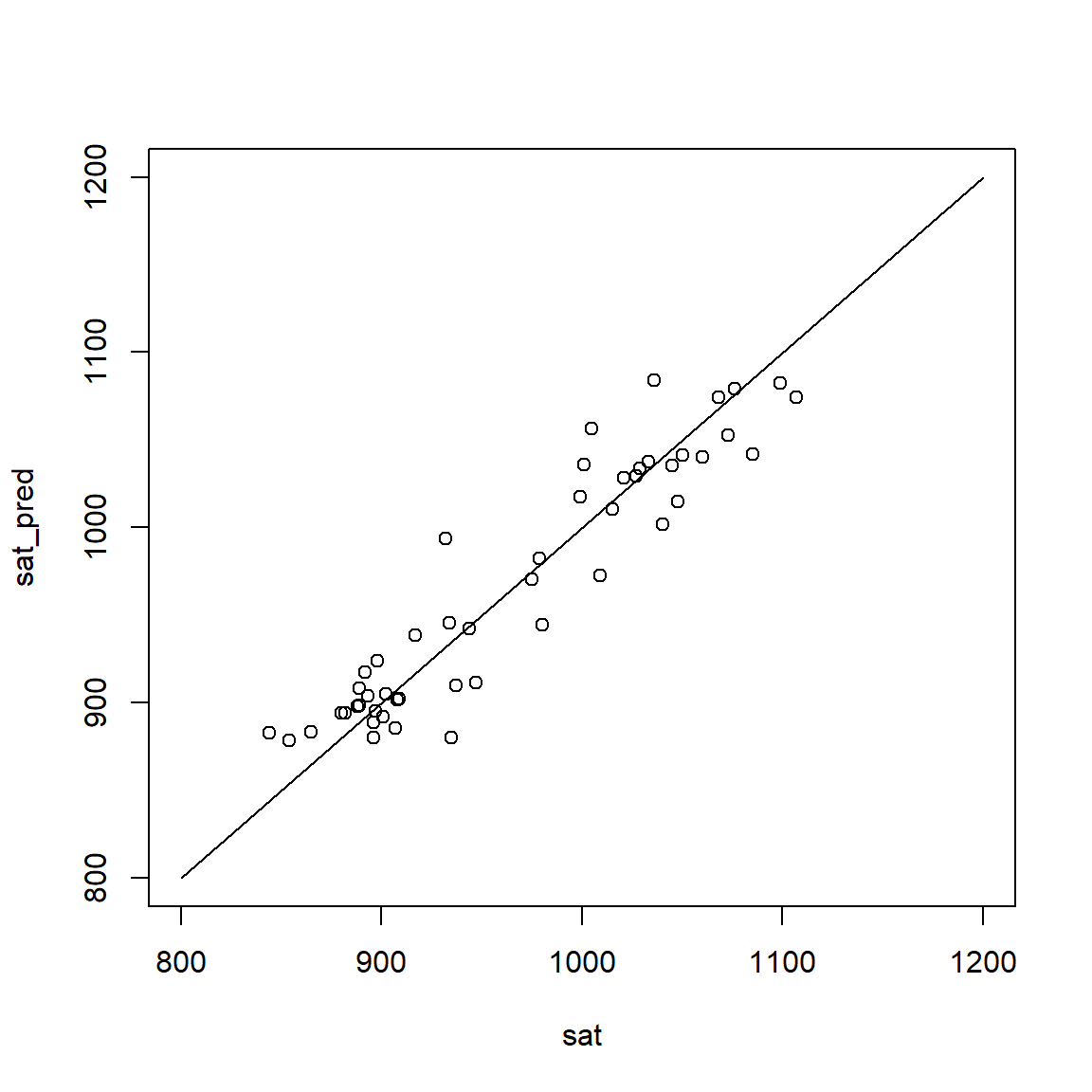

R <- cor(sat, sat_pred)
R2 <- R^2
rms_error <- sqrt(mean((sat_pred - sat)^2))
round(c(R = R, R2 = R2, rms_error = rms_error), 3)

        R        R2 rms_error 
    0.941     0.886    24.995 

Check of residuals

Our regression model implies that data are normally distributed around predicted values. This means that residuals (observed value - predicted mean value) should be evenly spaced around zero. A way to check this is to plot residuals versus fitted values.

adj_fitted <- adjusted$fitted
adj_res <- adjusted$residuals
plot(adj_fitted, adj_res, xlab = "SAT score (fitted values)", 
     ylab = "Residuals (Adjusted model)")
abline(h = 0, lty = 2)

# Smoothing estimated, should be approx flat around y = 0
lines(lowess(adj_res ~ adj_fitted), col = "red", lty = 3)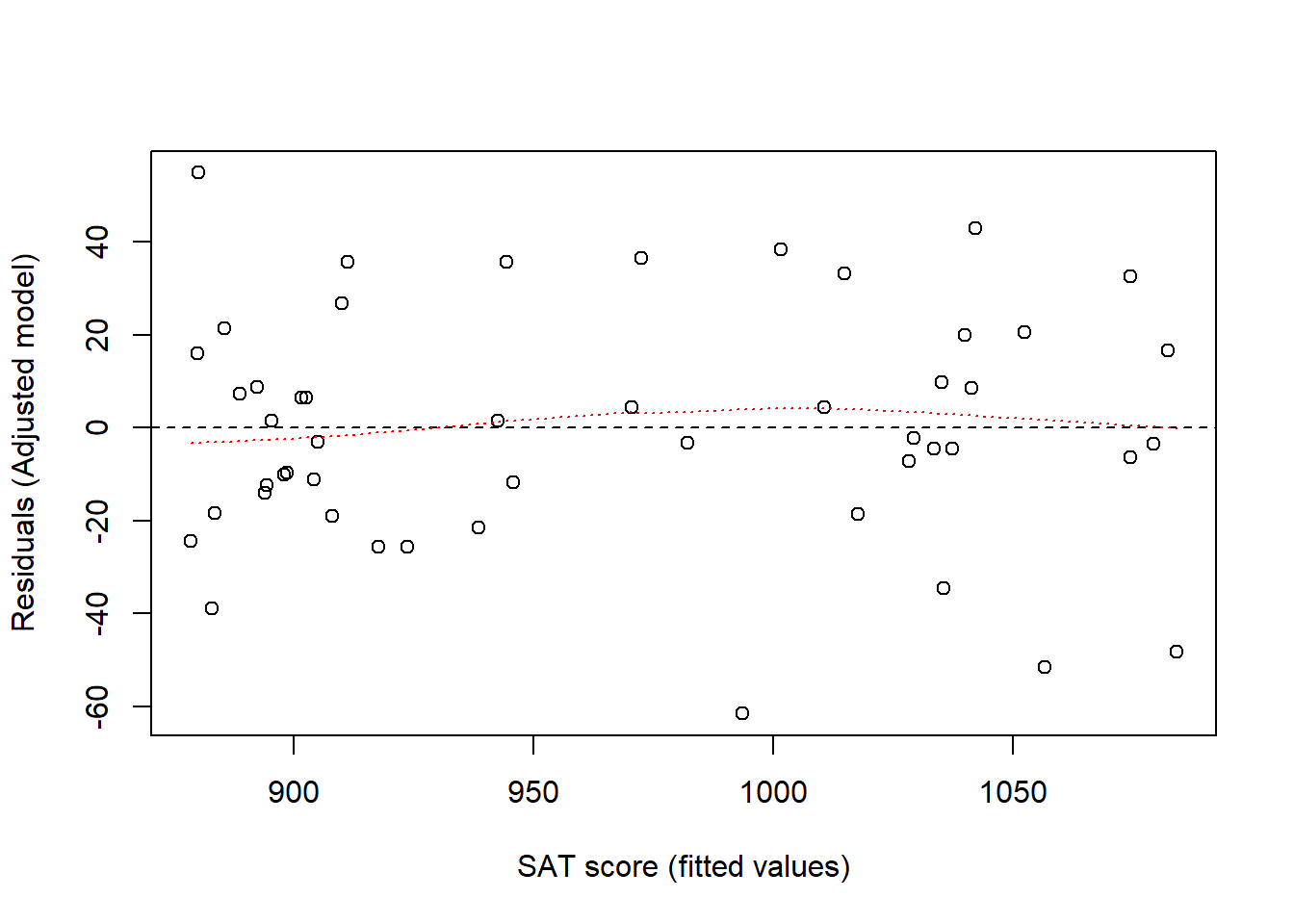 

With small data sets it may be useful to check each residual. Here I just plot residuals for each state, to see for which state the model fitted best and worst.

adj_res <- adjusted$residuals
adj_res_sorted <- adj_res[order(adj_res)]
plot(adj_res_sorted, xaxt='n', xlab = '', ylab = "Residual", ylim = c(-70, 70))
lines(c(0, 51), c(0, 0), lty = 2)

state_sorted <- state[order(adj_res)]
axis(1, at = 1:length(adj_res_sorted), labels = state_sorted, las = 2, cex = 0.5)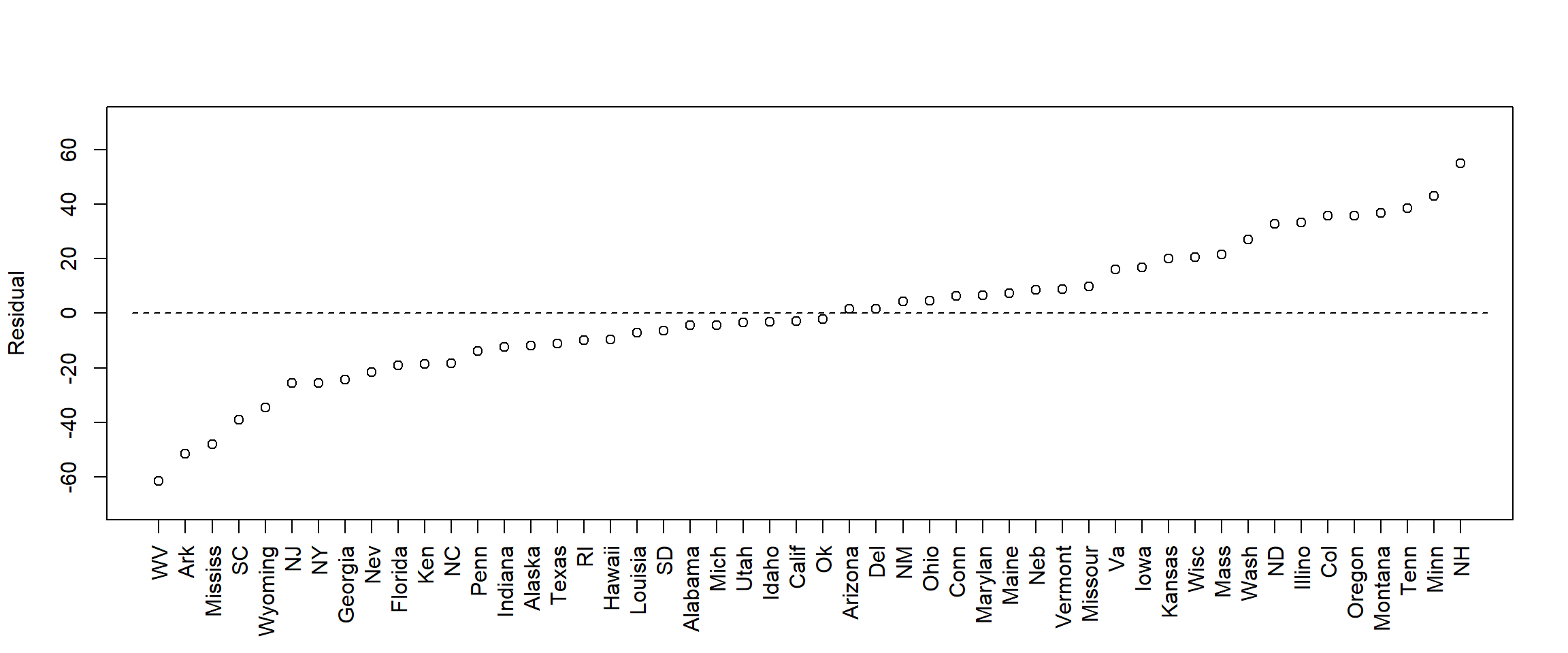

More on diagnostic plots below (section: Regression diagnostics).

More models

Here modeling as above but with additional variables. Always keep risk of over-adjustment bias in mind! Another issue is the number of data points, the largest model below has 5 parameters for the 50 data points; this is probably OK. An old rule-of-thumb is at least 10 data points per estimated parameter (Note:
With Bayesian estimation you can have fewer, and compensate for lack of data with stricter priors.)

# Recalculating and renaming the two models from above 
m1 <- glm(sat ~ expend)  # Crude above
m2 <- glm(sat ~ expend + psatlog) # Adjusted above
m3 <- glm(sat ~ expend + psatlog + ptratio)
m4 <- glm(sat ~ expend + psatlog + salary)
m5 <- glm(sat ~ expend + psatlog + ptratio + salary)

m1b <- c(m1$coefficients[2], confint(m1)[2, ])
m2b <- c(m2$coefficients[2], confint(m2)[2, ])
m3b <- c(m3$coefficients[2], confint(m3)[2, ])
m4b <- c(m4$coefficients[2], confint(m4)[2, ])
m5b <- c(m5$coefficients[2], confint(m5)[2, ])

# create empty plot 
plot(0, xaxt = "n", xlim = c(0.5,5.5), ylim = c(-50, 50), 
     pch = "", xlab = "", 
     ylab = "Linear regression coefficient (SAT / Expend)")
# Add x-axis labels
axis(1, at = 1:5, las = 2, cex = 0.7, 
     labels = c('Expend', 'Expend+\nlogpSAT', 'Expend+\nlogpSAT+\nPTratio', 
                'Expend+\nlogpSAT+\nSalary', 
                'Expend+\nlogpSAT+\nPTratio+\nSalary'))


# Add dotted line (lty = 2) at no effect: regression coefficient = 0
lines(c(-0.2,5.7), c(0,0), lty = 2)

# Add CI for models
add_ci <- function(m, xpos = 1){
  arrows(x0 = xpos, x1 = xpos, y0 = m[2], y1 = m[3], 
       angle = 90, code = 3, length = 0.1)
  points(xpos, m[1], pch = 21, bg = "grey")
}
add_ci(m1b, xpos = 1)
add_ci(m2b, xpos = 2)
add_ci(m3b, xpos = 3)
add_ci(m4b, xpos = 4)
add_ci(m5b, xpos = 5)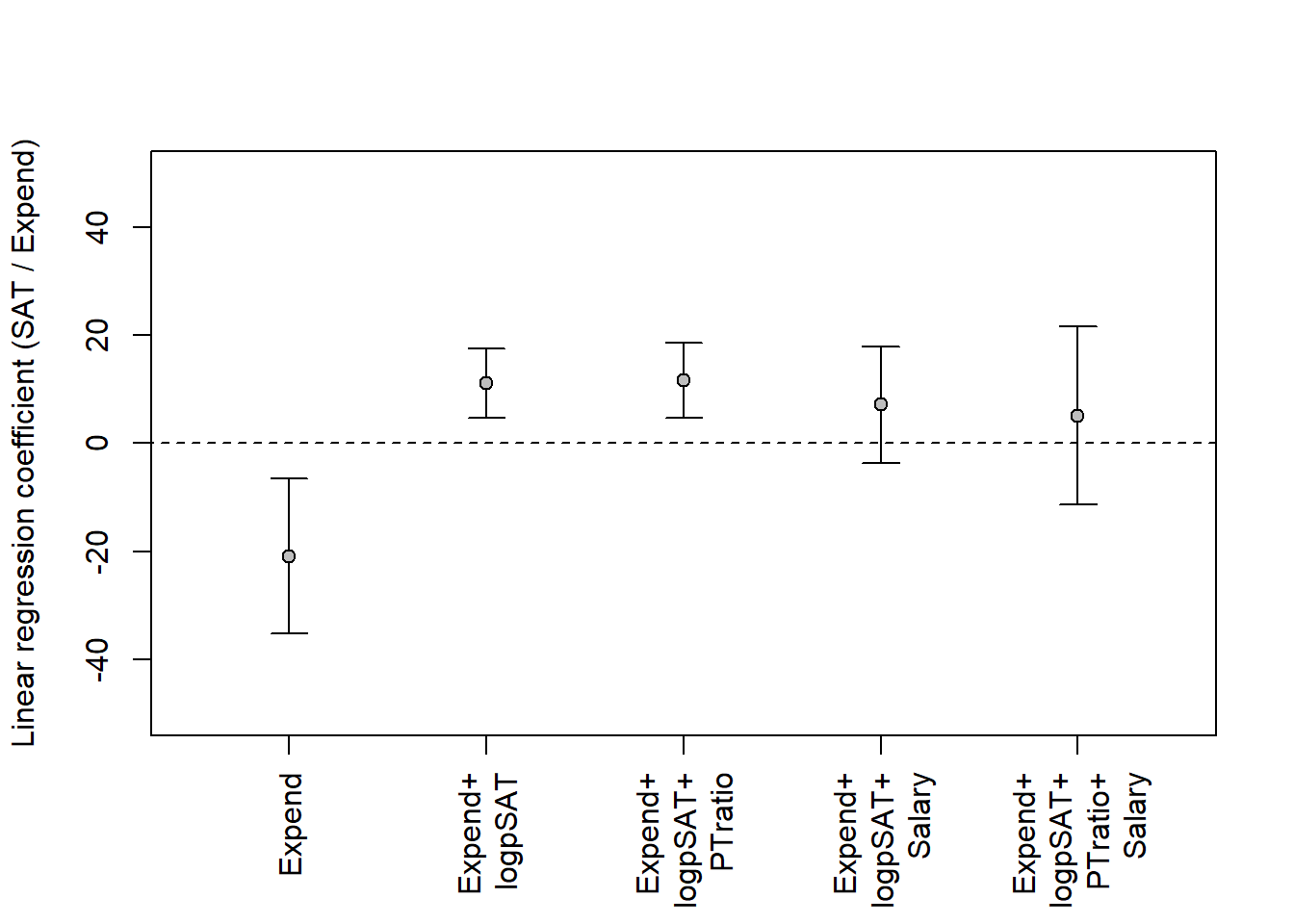

Which of these two is your model?

library(dagitty)

Warning: package 'dagitty' was built under R version 4.4.3

dag1 <- dagitty( "dag {
   expend -> sat
   sat <- pratio <- U -> expend
   expend -> salary -> sat
   expend -> ptratio -> sat
}")

dag2 <- dagitty( "dag {
   expend -> sat
   sat <- pratio <- U -> expend
   expend <- salary -> sat
   expend <- ptratio -> sat
}")

coordinates(dag1) <- list(
  x = c(expend = 1, U = 1.5, pratio = 2.5, salary = 2.5, ptratio = 2.5, sat = 4),
  y = c(expend = 3, U = 1.5, pratio = 2, salary = 1, ptratio = 2.5, sat = 3))

coordinates(dag2) <- list(
  x = c(expend = 1, U = 1.5, pratio = 2.5, salary = 2.5, ptratio = 2.5, sat = 4),
  y = c(expend = 3, U = 1.5, pratio = 2, salary = 1, ptratio = 2.5, sat = 3))

par(mfrow = c(1, 2))
plot(dag1)
plot(dag2)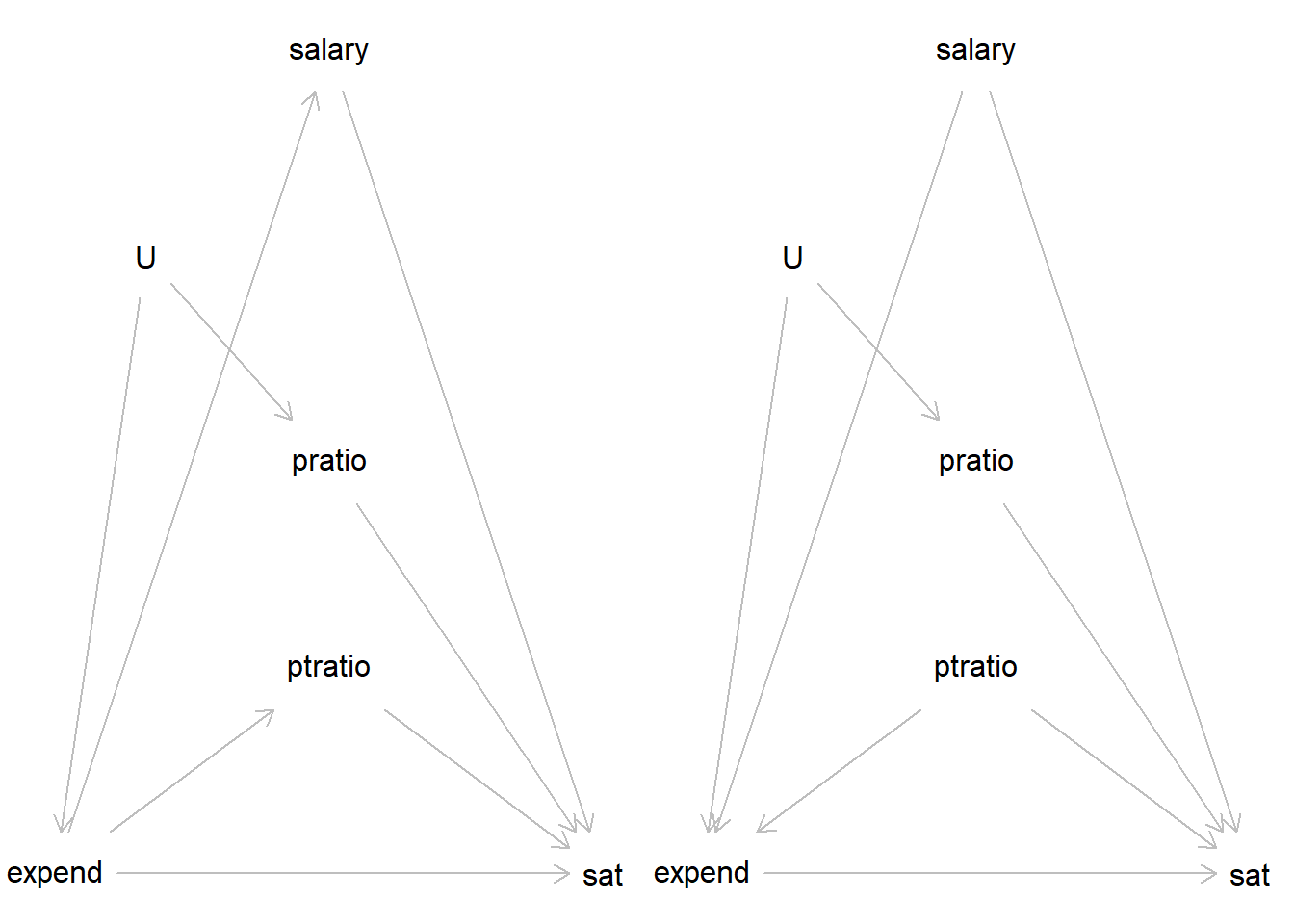

12.2 Assumptions

See Gelman et al. (2021), Chapter 11, Section 11.1 for an excellent review of regression assumptions. They list a number of assumptions, in order of importance. Here a brief version:

1. Validity. Make sure your data maps the research question you are trying to answer. If your data contain test-scores, consider the validity of these (are they really measuring what they purport to do?). If your goal is causal inference, then the selection of covariates is crucial, both included and omitted variables may induce bias. Select your covariates from a causal theory (e.g., a Directed Acyclical Graph). Be aware of the causal nature of the interpretation of a regression coefficient as “the effect of a variable with all else held constant”. This causal interpretation often make no sense.
2. Representativeness. If you want to generalize to the population, your sample should be representative of the population. Unrepresentative sample is not only a threat to external validity, but may also be a threat to internal validity, e.g., collider bias (a form a selection bias). Often the population is thought of as an infinite hypothetical superpopulation, so the question arises also when you conduct analysis on all members of a population (maybe you want to be able to predict future members of the population, etc.)
3. Additivity and linearity These are the most important mathematical assumptions of the general linear model. Note that many non-linear relationships can be made linear by suitable transformations
4. Independence of errors. We assume that observations are sampled independent of each other.
5. Equal variance of errors This is \(\sigma\) in our linear model, it is assumed to be constant for all levels of predictors. Non-linear transformations may help, for example, the log transform if the variability around the line is proportional to the size of the predicted value.
6. Normality of errors This is the assumption that the outcome is normally distributed given our predictors, that is, the distribution of points around a given point of the regression line is normally distributed. For the prediction of the regression line (i.e., mean values for a given value of x), this is not a very important assumption.

12.3 Regression diagnostics

There are several ways to check your model. In the SAT-data example above, these three plots were used:

1. Display regression line(s) as a function of one predictor. This is the best way to understand the implications of our model. Consider several plots, each with a different value of one or several other key variables. This is crucial for understanding interaction models. See examples above, for age-weight data and for the school data.
2. Residual plots. For small data sets, it may be a good idea to rank order residuals to check them one one by one (see school-data example above). For large data sets, a plot of residuals versus predicted values can indicate problems with your model. We want outcomes to be evenly distributed along the regression line, resulting in an even residual plot (see Gelman et al. (2021), figs. 11.6-8).
3. Predicted value against observed data. Gives an idea of how well the overall model fits the data, see example above from the school data.

Advanced - Regression diagnostics

With Bayesian estimation, several other diagnostic plots are available. Bayesian models are data-generative, that is, they can be used to generate simulated data in accordance with your model. Comparing these simulated data (your model implications) with your actual outcome data is a fundamental way to check your. A good model should generate data that looks a lot like the data you observed (the data it was supposed to model). Such plots may guide you to aspects of the model that seem inconsistent with your model.
We have already discussed one such plot above (3. Predicted against observed data), but that one was limited to point-estimates of predicted means. A more advanced plot will simulate new data, taking into account uncertainty in predicted means (\(\mu_i\)) and uncertainty in the predicted variation around means (\(\sigma\)). See, Gelman et al., Section 11.4 for a simple illustration.

Below I illustrate using models of the SAT-data discussed above. To do this, I need first to fit the models in stan_glm() from the rstanarm packages.

# Crude model
m1 <- stan_glm(sat ~ expend, data = d, refresh = 0)  
print(m1)

stan_glm
 family:       gaussian [identity]
 formula:      sat ~ expend
 observations: 50
 predictors:   2
------
            Median MAD_SD
(Intercept) 1088.9   44.1
expend       -20.8    7.3

Auxiliary parameter(s):
      Median MAD_SD
sigma 70.5    7.2  

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg

# Adjusting for psat
m2 <- stan_glm(sat ~ expend + psatlog, data = d, refresh = 0) 
print(m2)

stan_glm
 family:       gaussian [identity]
 formula:      sat ~ expend + psatlog
 observations: 50
 predictors:   3
------
            Median MAD_SD
(Intercept) 1147.1   16.3
expend        11.1    3.3
psatlog      -78.1    4.7

Auxiliary parameter(s):
      Median MAD_SD
sigma 26.1    2.6  

------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanreg

I then extract samples from the posterior distribution of model parameters.

# Extract samples, you may also use as.matrix() as Gelman et al (e.g., p. 163)
 
# Crude model
ss1 <- as.data.frame(m1) 
head(ss1)

  (Intercept)    expend    sigma
1    1115.356 -27.21964 57.91113
2    1052.209 -13.09154 83.51162
3    1137.713 -30.30710 62.34097
4    1116.702 -23.27341 71.25001
5    1133.792 -26.80801 79.69628
6    1051.870 -15.75319 57.69220

# Adjusted model
ss2 <- as.data.frame(m2)
head(ss2)

  (Intercept)    expend   psatlog    sigma
1    1125.964 16.346956 -82.72654 27.01791
2    1159.490  8.475829 -75.83672 23.89718
3    1127.625 12.157837 -74.88251 27.75706
4    1133.542 13.470384 -78.22500 28.97512
5    1146.142 16.611083 -87.31651 27.44121
6    1146.331  7.548495 -73.11641 25.40585

Then I create simulated data sets, one for each row of the data frame with sampled parameter values. Each row is one plausible model.

ndraws <- nrow(ss1)
n <- length(d$sat)

# Model m1
yrep1 <- array(NA, dim = c(ndraws, n))
x <- d$expend

for (j in 1:ndraws){
  yrep1[j, ] <- rnorm(n, 
                     mean = ss1$`(Intercept)` + ss1$expend*x,
                     sd = ss1$sigma)
}
  
# Model m2
yrep2 <- array(NA, dim = c(ndraws, n))
x1 <- d$expend
x2 <- d$psatlog

for (j in 1:ndraws){
  yrep2[j, ] <- rnorm(n, 
                     mean = ss2$`(Intercept)` + ss2$expend*x1 + ss2$psatlog*x2,
                     sd = ss2$sigma)
}

# Look at yrep arrays
str(yrep1)

 num [1:4000, 1:50] 997 932 1055 1134 1045 ...

str(yrep2)

 num [1:4000, 1:50] 1053 1004 1034 1056 1055 ...

The objects yrep1 and yrep2 contain 4000 simulated data sets, each with 50 observations (because our data set contained 50 observations)

Finally, I may plot observed data (y) and simulations (yrep), e.g., using kernel density plots as below.

set.seed(123)
par(mfrow = c(1, 2))

# Model 1: Crude
plot(density(d$sat), xlim = c(700, 1300),
     ylim = c(0, 0.008), main = "Crude model", xlab = "SAT score")
for (j in sample(1:ndraws, 30)) {
  lines(density(yrep1[j, ]), col = rgb(1, 0, 0, 0.2))
}


# Model 2: Adjusted
plot(density(d$sat), xlim = c(700, 1300),
     ylim = c(0, 0.008), main = "Adjusted model", xlab = "SAT score")
for (j in sample(1:ndraws, 30)) {
  lines(density(yrep2[j, ]), col = rgb(1, 0, 0, 0.2))
}

# Legend
lines(c(1100, 1150), c(0.008, 0.008))
lines(c(1100, 1150), c(0.0075, 0.0075), col = "red")
text(1160, 0.008, labels = "y",    pos = 4, cex = 0.7)
text(1160, 0.0075, labels = "yrep", pos = 4, cex = 0.7)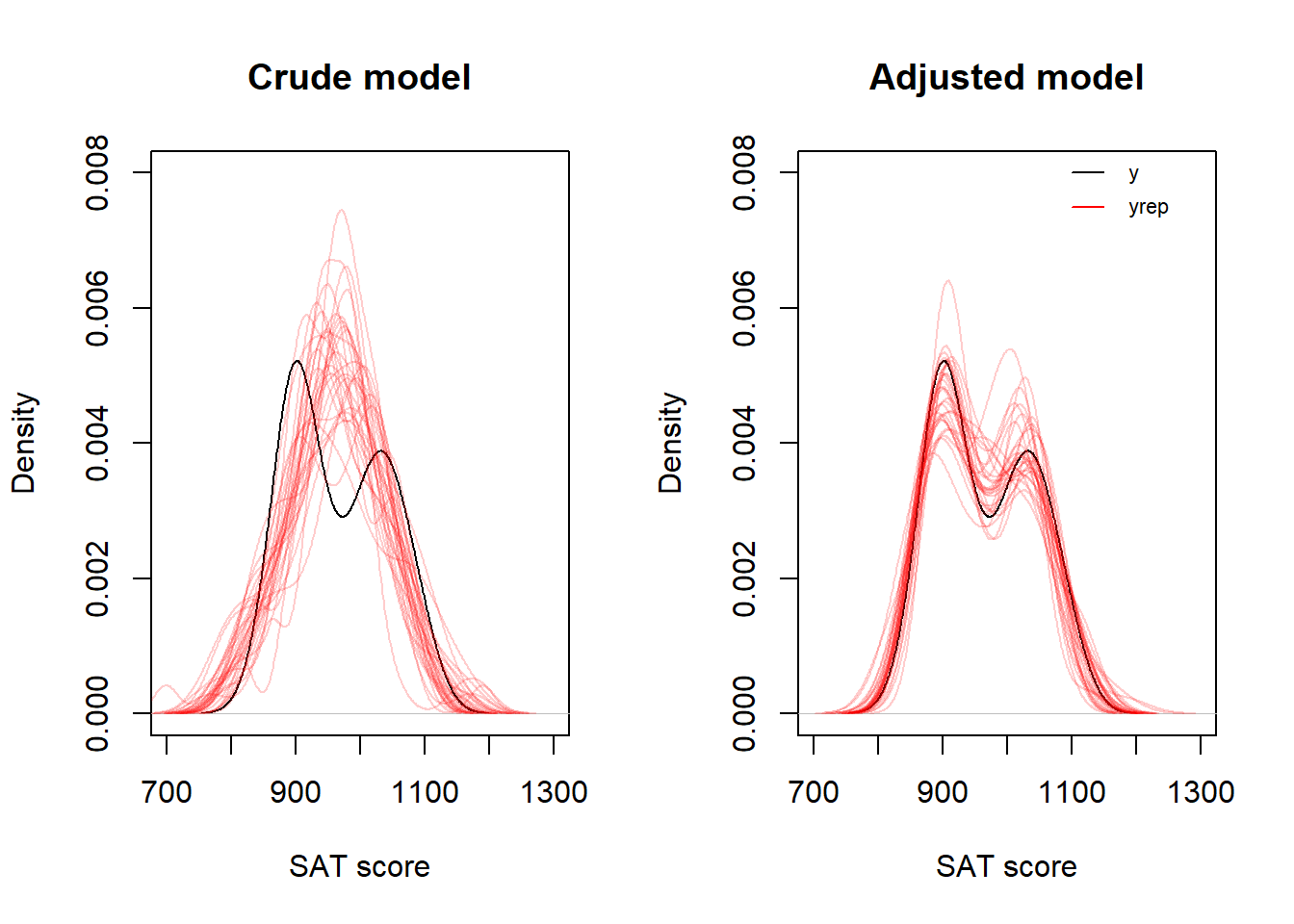

A faster way to simualte data sets (yrep) is to use the poster_predict() function in rstanarm. Here a plot of distribution of IQRs over 4000 sets of yrep (black line), compared to the IQR of the observed data, y (blue line).

yrep1 <- posterior_predict(m1)
yrep2 <- posterior_predict(m2)

par(mfrow = c(1, 2))
iqr1 <- apply(yrep1, 1, IQR)
plot(density(iqr1), main = "Crude model IQR", xlim = c(20, 200), xlab = "IQR")
abline(v = IQR(d$sat), col = "blue")

iqr2 <- apply(yrep2, 1, IQR)
plot(density(iqr2), main = "Adjusted model IQR", xlim = c(20, 200), xlab = "IQR")
abline(v = IQR(d$sat), col = "blue")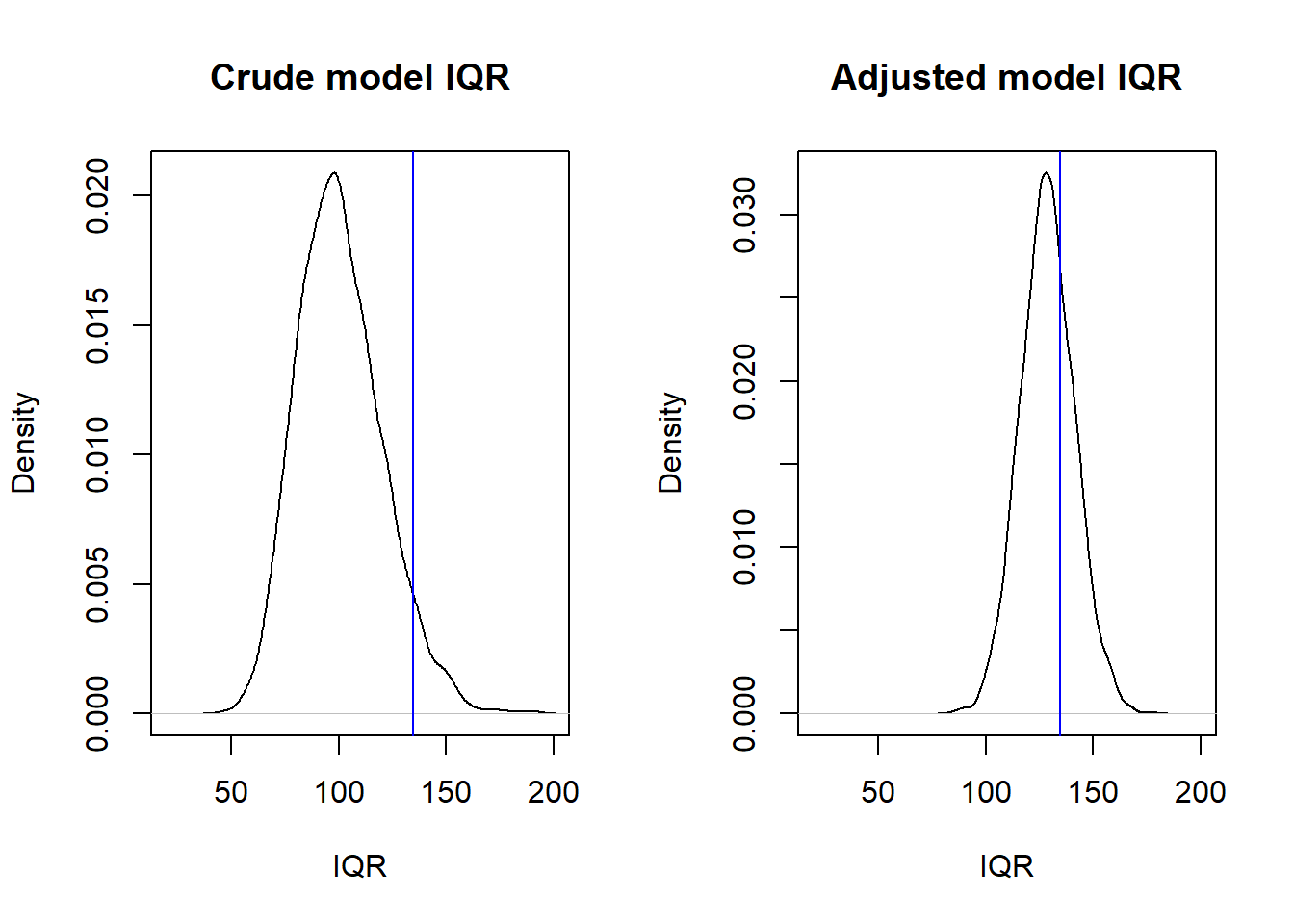

12.4 Model fit

Models are often evaluated based on how well they fit data. For linear models, common measures of fit are derived from residuals. A residual, \(r_i\), is defined as

\(r_i = y_i - \hat{y_i}\), where \(\hat{y_i}\) is the model’s prediction for an observation \(y_i\).

When the model is evaluated using the same data on which it was fitted (or “trained”), this may be referred to as internal or in-sample model evaluation. In this approach, the observed data is used twice—first to fit the model and then to assess its performance based on residuals. Two common measures for in-sample fit are the residual standard deviation (\(\hat{\sigma}\)) and the proportion of explained variance, \(R^2\).

One key limitation of in-sample fit is the risk of overfitting, where the model captures random patterns specific to a particular data set. As a result, an overfitted model may perform poorly when applied to new, unseen data that lacks those specific random errors.

When the model is evaluated using a new data set, this may be referred to as external or out-of-sample model evaluation. A general term for this is cross-validation as briefly discussed below.

In-sample: Residual standard deviation and explained variance

The residual standard deviation, \(\hat{\sigma}\), is an estimate of the \(\sigma\) of the general linear model (see these notes, Section 8.4). \(\sigma\) is the dispersion of values around the population mean associated with specific values of the predictors. We may use \(\hat{\sigma}\) as a measure of the unexplained variation in the data.

The amount of variance “explained” by the model, \(R^2\). This is a standardized measure that relates \(\hat{\sigma}^2\) to the sample variance of the outcome, \(s^2_y\): \(R^2 = 1 - (\hat{\sigma}^2/s^2_y)\). If equal, then \(R^2 = 0\), if \(\hat{\sigma}^2 = 0\), all data points fall on the regression line, then \(R^2 = 1\).

For more on this, see Gelman et al. (2021), section 11.6.

Out-of-sample: Cross-validation

Not covered in this course, but important, so the ambitious student should consult Gelman et al. (2021), section 11.7-11.8.

12.5 Ten quick tips ro regression modelling

Appendix B of Gelman et al. (2021) give 10 tips to improve your regression modeling. Excellent suggestions, read carefully! And remember where you read it, so you can revisit as your modelling skills guest more advanced and your models more complex. Here is a short version of my interpretation of their tips:

1. Think about variation and replication. If possible, fit your model to different data sets to get a sense of variation across studies and problems. One study is seldom enough to seriously answer your research question.
2. Forget about statistical significance. “Forget about p-values, and forget about whether your confidence intervals exclude zero” (p. 493). Dichotomous thinking is throwing away useful information about uncertainty. So, resist dichotomous thinking and embrace uncertainty (cf. Amrhein et al. (2019))
3. Graph the relevant and not the irrelevant. See the book for many useful ways of visualizing your model and data. Do not forget to plot model implications to understand your model. And be prepared to explain any graph you show (if you can’t, it is probably not a useful plot).
4. Interpret regression coefficients as comparisons. Avoid the term “effect” of regression coefficients unless you really mean causal effect. But you can always think of a predictor coefficient as a difference in the outcome for one unit difference in the predictor (keeping other predictors constant).
5. Understand statistical methods using fake-data simulation. Nowadays, data simulation is indispensable tool for the data analyst. Simulation is a way of understanding our models before we start fitting them to data, and it is a way of evaluating how well they fit data. For complex models, you should use simulations to test your code and make sure that you can recovery true parameters.
6. Fit many models. Fitting a set of models, from simple to complex is a way to understand our models and our data. Always be aware of the risk of over-fitting and under-fitting, and, if your goal is causal inference, of introducing bias with incorrect choice of predictors.
7. Set up a computational work flow. For complex models and large data sets, you will encounter computational issues. It may just take too long time to fit your model, or the software will refuse to do as you say (resulting in error messages). Consider simple models, maybe separate models for subsets of your data, and always check you model against fake-data simulations.
8. Use transformations. “Consider transforming just about every variable in sight” (p. 496). In addition to linear and non-linear transformations of single variables, also consider interactions and combinations of variables. As long as you model make sense it is worth testing and comparing to other models.
9. Do causal inference in a targeted way, not as a byproduct of a large regression. Select predictors carefully if your goal is causal inference. Use Directed Acyclical Graphs to hep you think clearly about causation with many variables, especially, of course, for non-experimental data.
10. Learn methods through live examples. Learn modelling by applying to problems that you found interesting. “Know your data, your measurements, and your data-collection procedure. … Understand the magnitudes of your regression coefficients, not just their signs. You will need this understanding to interpret your findings and catch things that go wrong” (p. 496).

Practice

The practice problems are labeled Easy (E), Medium (M), and Hard (H), (as in McElreath (2020)).

Easy

12E1. In a linear regression model predicting weight [kg] as a function of age [y], the age variable used in the linear regression model was transformed to:

\(age_{transformed} = 10(age - 40)\)

Why? (two reasons)

12E2. Centering of a predictor in a multiple regression model will change the intercept of the model. What happens to the regression coefficients (slopes)?

Medium

12M1. Go back to the kidiq data discussed in chapter 10 of these notes. Do diagnostic plots. Specifically:

1. Plot model prediction versus observed values, separately for mom_hs = 0 and mom_hs = 1.(cf. Gelman et al, Fig. 11.4)
2. Residuals versus fitted values (cf. Gelman et al, Fig. 11.7 left panel), with separate symbols for mom_hs = 0 and mom_hs = 1.

Comment on what you see.

Hard

12H1. Go back to the model in 12M1. Plot kernel densities for observed kidiq (y) overlaid with densities for simulated data sets (yrep). Do for the whole data set, and separately for mom_hs = 0 and mom_hs = 1.

Use the function posterior_predict() to generate simulated data (yrep). Compare your plot with the corresponding plot generate using the function pp_check()

12H2. Redo the density plot from 12H1, but now from scratch. That is, don’t use posterior_predict() to generate samples, do it “by hand” from extracted samples (as.data.frame(modelfit) or as.matrix(modelfit)). Se example above, and in Gelman et al (p. 163)

(Session Info)

sessionInfo()

R version 4.4.2 (2024-10-31 ucrt)
Platform: x86_64-w64-mingw32/x64
Running under: Windows 11 x64 (build 26100)

Matrix products: default


locale:
[1] LC_COLLATE=Swedish_Sweden.utf8  LC_CTYPE=Swedish_Sweden.utf8   
[3] LC_MONETARY=Swedish_Sweden.utf8 LC_NUMERIC=C                   
[5] LC_TIME=Swedish_Sweden.utf8    

time zone: Europe/Stockholm
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] dagitty_0.3-4   rstanarm_2.32.1 Rcpp_1.0.14    

loaded via a namespace (and not attached):
 [1] tidyselect_1.2.1     dplyr_1.1.4          farver_2.1.2        
 [4] loo_2.8.0            fastmap_1.2.0        tensorA_0.36.2.1    
 [7] shinystan_2.6.0      promises_1.3.3       shinyjs_2.1.0       
[10] digest_0.6.37        mime_0.13            lifecycle_1.0.4     
[13] StanHeaders_2.32.10  survival_3.7-0       magrittr_2.0.3      
[16] posterior_1.6.1      compiler_4.4.2       rlang_1.1.6         
[19] tools_4.4.2          igraph_2.1.4         yaml_2.3.10         
[22] knitr_1.50           htmlwidgets_1.6.4    pkgbuild_1.4.8      
[25] curl_6.4.0           plyr_1.8.9           RColorBrewer_1.1-3  
[28] dygraphs_1.1.1.6     abind_1.4-8          miniUI_0.1.2        
[31] grid_4.4.2           stats4_4.4.2         xts_0.14.1          
[34] xtable_1.8-4         inline_0.3.21        ggplot2_3.5.2       
[37] scales_1.4.0         gtools_3.9.5         MASS_7.3-61         
[40] cli_3.6.5            rmarkdown_2.29       reformulas_0.4.1    
[43] generics_0.1.4       RcppParallel_5.1.10  rstudioapi_0.17.1   
[46] reshape2_1.4.4       minqa_1.2.8          rstan_2.32.7        
[49] stringr_1.5.1        shinythemes_1.2.0    splines_4.4.2       
[52] bayesplot_1.13.0     parallel_4.4.2       matrixStats_1.5.0   
[55] base64enc_0.1-3      vctrs_0.6.5          V8_6.0.4            
[58] boot_1.3-31          Matrix_1.7-1         jsonlite_2.0.0      
[61] crosstalk_1.2.1      glue_1.8.0           nloptr_2.2.1        
[64] codetools_0.2-20     distributional_0.5.0 DT_0.33             
[67] stringi_1.8.7        gtable_0.3.6         later_1.4.2         
[70] QuickJSR_1.8.0       lme4_1.1-37          tibble_3.3.0        
[73] colourpicker_1.3.0   pillar_1.10.2        htmltools_0.5.8.1   
[76] R6_2.6.1             Rdpack_2.6.4         evaluate_1.0.3      
[79] shiny_1.11.1         lattice_0.22-6       markdown_2.0        
[82] rbibutils_2.3        backports_1.5.0      threejs_0.3.4       
[85] httpuv_1.6.16        rstantools_2.4.0     gridExtra_2.3       
[88] nlme_3.1-166         checkmate_2.3.2      xfun_0.52           
[91] zoo_1.8-14           pkgconfig_2.0.3     

Amrhein, V., Greenland, S., & McShane, B. (2019). Retire statisticial significance. Nature, 567, 305–307.

Gelman, A., Hill, J., & Vehtari, A. (2021). Regression and other stories. Cambridge University Press.

Guber, D. (1999). Getting what you pay for. Journal of Statistics Education, 7(2).

McElreath, R. (2020). Statistical rethinking: A bayesian course with examples in r and stan. Chapman; Hall/CRC.